Inégalité de Cauchy-Swharz
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 12 Avr 2012, 15:15
par Cryptocatron-11 » 12 Avr 2012, 15:15
Bonjour,
Je comprends pas la démo de mon cours concernant l'inégalité de Cauchy-Swharz. On a :

Je comprends pas déjà comment il passe de la deuxième à la troisième ligne ... J'aurais plutôt cru que
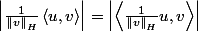
Non ?
Bon continuons ...
Il pose

Bon bah ça OK
D'ou

Puis

Et là non plus je comprends pas du tout comment il passe de ces deux dernières inégalités ...
-
Mystifree
- Messages: 3
- Enregistré le: 12 Avr 2012, 15:24
-
 par Mystifree » 12 Avr 2012, 15:25
par Mystifree » 12 Avr 2012, 15:25
Bonjour.
Pour le passage de la deuxième à la troisième ligne de ta démonstration, tu peux pas justifier ça par la bilinéarité du produit scalaire (avec ici la linéarité selon la 2° coordonnée) ?
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 12 Avr 2012, 15:30
par Cryptocatron-11 » 12 Avr 2012, 15:30
Ouais. Par contre si on est dans un C-ev , je sais pas si on peut utiliser cette axiome là ... si ?
Et pour ma deuxième question , tu peux m'expliquer ce passage ?
-
Mystifree
- Messages: 3
- Enregistré le: 12 Avr 2012, 15:24
-
 par Mystifree » 12 Avr 2012, 15:46
par Mystifree » 12 Avr 2012, 15:46
J'ai juste eu l'idée en relisant ta démonstration pour la bilinéarité, après j'ai travaillé la démonstration uniquement sur le corps des fonctions continues (ou CPM) de R. Il y a une histoire de "semi-linéarité" du produit scalaire sur les espaces complexes, à vérifier.
En ce qui concerne ton deuxième point de passage, c'est pas, pour en revenir au corps des fonctions continues, analogue au moment ou on reprend la forme (Int(f+lambda*g)²) ?
-
gdlrdc
- Membre Relatif
- Messages: 160
- Enregistré le: 24 Jan 2009, 18:11
-
 par gdlrdc » 12 Avr 2012, 16:12
par gdlrdc » 12 Avr 2012, 16:12
Pas de probleme car on prend le module et tu sais que module de z = module du conjugué de z.
-
Rifl3
- Membre Naturel
- Messages: 59
- Enregistré le: 02 Avr 2012, 15:50
-
 par Rifl3 » 12 Avr 2012, 16:12
par Rifl3 » 12 Avr 2012, 16:12
Pour le 1er passage c'est bien valable dans C. Car le produit scalaire est sesquilinéaire, donc semi-linéaire à gauche et linéaire à droite :
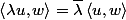
pour la semilinéarité a gauche et
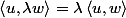
pour la linéarité à droite
Fin juste un des axiomes.
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 12 Avr 2012, 16:35
par Cryptocatron-11 » 12 Avr 2012, 16:35
Mystifree a écrit:En ce qui concerne ton deuxième point de passage, c'est pas, pour en revenir au corps des fonctions continues, analogue au moment ou on reprend la forme (Int(f+lambda*g)²) ?
Bah je sais pas du tout vu que j'en suis pas encore là dans mon cours ...
-
Blueberry
- Membre Relatif
- Messages: 243
- Enregistré le: 04 Mar 2007, 09:51
-
 par Blueberry » 12 Avr 2012, 17:54
par Blueberry » 12 Avr 2012, 17:54
Il manque deux étapes entre les deux lignes (je suis assez surpris)
| u.w | ² <= || u || ²
et si tu note p(u) = |u.w|w, on peut réécrire la ligne précédente :
||p(u)|| ² <= || u - p(u)|| ² + ||p(u)||²
ce qui donne bien 0 <= ||u - |u.w|w||²
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 12 Avr 2012, 18:11
par Cryptocatron-11 » 12 Avr 2012, 18:11
Blueberry a écrit:Il manque deux étapes entre les deux lignes (je suis assez surpris)
| u.w | ² <= || u || ²
et si tu note p(u) = |u.w|w, on peut réécrire la ligne précédente :
||p(u)|| ² <= || u - p(u)|| ² + ||p(u)||²
ce qui donne bien 0 <= ||u - |u.w|w||²
J'ai du mal là aussi à voir le passage avec p(u)
J'ai essayé avec l'I.T mais j'arrive pas à retomber sur ton ||p(u)|| ² <= || u - p(u)|| ² + ||p(u)||²
:mur:
-
Blueberry
- Membre Relatif
- Messages: 243
- Enregistré le: 04 Mar 2007, 09:51
-
 par Blueberry » 12 Avr 2012, 19:16
par Blueberry » 12 Avr 2012, 19:16
[quote="Cryptocatron-11"]J'ai du mal là aussi à voir le passage avec p(u)
J'ai essayé avec l'I.T mais j'arrive pas à retomber sur ton ||p(u)|| ² )
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
