Incomprehension Somme Riemann/Integrale

[SinusSlide]

Bonjour, je ne comprends pas ce qui suit dans un corrigé.. jcrois que jcapte rien aux integrales ?

Enoncé:
Soit f une fonction continue, positive et décroissante sur R+*
on pose S(n)=f(1)+...+f(n) et T(n)= Intégrale[1,n]f(t)dt

Je ne comprends pas la 1ere phrase du corrigé:
f décroissante sur R+* donc:
f(k+1)<ou=Intégrale[k,k+1]<ou=f(k) , k € N*

l'Intégrale[k,k+1], c'est bien f(k)+..infini..+f(k+1) donc pour moi, cette somme est supérieur à f(k) ?

Question annexe que je comprends pas entre l'intégrale et la somme de riemann:

Par exemple, on peut considérer S(n) d'une part comme la somme des valeurs de la fonction en x =1,2...n mais d'autre part on peut considérer que c'est S(n)=1*f(1)+...+1*f(n), c'est à dire la somme des aires des rectangles de hauteur f(x) et longueur 1... du coup on peut amener à dire que par exemple f(1)=aire du rectangle du hauteur f(1) et de longueur 1, ce qui n'a pas de sens ??
jsuis vraiment perdu...

[Maxmau]

Bj
Sur [k,k+1] f est coincée entre les constantes f(k+1) et f(k) (puisque f est décroissante)
Donc l'intégrale de f sur [k,k+1] est coincée entre l'aire du rectangle de longueur 1 et de hauteur f(k+1) et l'aire du rectangle de longueur 1 et de hauteur f(k)

[deltab]

Bonjour

Bonjour

... du coup on peut amener à dire que par exemple f(1)=aire du rectangle du hauteur f(1) et de longueur 1, ce qui n'a pas de sens ??

Indépendamment de l'exercice, quelle est l'aire d'un rectangle de largeur a>0 et de longueur 1?
et pour a=f(1)?

[SinusSlide]

Je crois avoir compris mon problème, merci.
Une intégrale ne se considère qu'en dimension 2 et donc considerer f(k) et f(k+1) en dimension 1 ds la premiere phrase du corrigé est une erreur !
Merci

[deltab]

Bonjour.

Je crois avoir compris mon problème, merci.
Une intégrale ne se considère qu'en dimension 2 et donc considerer f(k) et f(k+1) en dimension 1 ds la premiere phrase du corrigé est une erreur !
Merci

Apparemment tu n'as pas saisi ma remarque dans mon autre post. Quel est le problème si la longueur (ou la largeur) valait 1? (Quelle est l'aire d'un rectangle de longueur 10m et de largeur 1m? la valeur numérique de l'aire et celle de la longueur coïncident mais elles n''ont la même unité de mesure ( m^2 et mètre)

Tu n'as vu la relation entre et l'intégrale ni celle de et .

Sur l'intervalle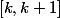 , on puisque f est décroissante et donc (proprété des intégrales)

[deltab]

Bonjour.

rectificatif

..... et donc (propriété des intégrales)

[SinusSlide]

Ca y'est cette fois j'ai compris ^^
On considère pas de manière hazardeuse d'un coté dimension 1 et de l'autre dimension 2 comme on souhaite dans la prop : f(k+1)dimension 2
f(k+1)<ou=Intégrale[k,k+1]<ou=f(k)

Merci !

Autre question Par rapport au contraire de la positivité d'une intégrale:
Si f est continue et <ou= 0 sur son Df alors avec a<b Int[a,b]f est <ou= 0 non ? OU ALORS, le calcul intégral est tjrs un calcul d'aires et ne peut donc être négatif ?

[deltab]

Bonsoir

Ca y'est cette fois j'ai compris ^^

Merci !

Autre question Par rapport au contraire de la positivité d'une intégrale:
Si f est continue et <ou= 0 sur son Df alors avec a<b Int[a,b]f est <ou= 0 non ? OU ALORS, le calcul intégral est tjrs un calcul d'aires et ne peut donc être négatif ?

Non!
La définition de l'intégrale est un passage à la limite sur les sommes de Riemann, cette limite peut donc exister ou ne pas exister.
Comme conséquence de cette définition, on peut citer:

1) Si f est continue sur [a,b], alors l'intégrale existe.

2) Si sur et si les deux intégrales et ALORS

3) Comme corollaire de 2):
Si sur [a,b] et si l'intégrale existe ALORS
Cette intégrale représente alors l'aire de la partie bornée du plan délimitée par l'axe des x (y=0), les deux droites x=a, x=b et le graphe de f.

Remarque:
On peut voir l'intégrale est une généralisation de la notion d'aire, l'intégrale représentera des aires pour des cas particuliers.
Il ne faut pas oublier l'utilisation de la notion d'intégrale en physique et dans d'autres sciences.

[SinusSlide]

3) Comme corollaire de 2):
Si sur [a,b] et si l'intégrale existe ALORS

Mais si on a g(x) <ou= 0 continue et definie sur Dg, a<b € Dg et son Int existe
alors
on peut définir f(x) = -g(x)
f est positive, son int existe et est positive et
Int g = - Int f = - par + = négative ??

[deltab]

Bonjour

Mais si on a g(x) <ou= 0 continue et definie sur Dg, a<b € Dg et son Int existe
alors
on peut définir f(x) = -g(x)
f est positive, son int existe et est positive et
Int g = - Int f = - par + = négative ??

Oui.
ça provient aussi de 2) et de l'équivalence .

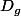Remarque: Tu as précisé que continue sur , et tu as supposé que l'intégrale de g sur[a,b] existe (c'est que j'ai compris en te lisant,) l'existence de l'intégrale de g sur[a,b] provient alors de 1) ( on rappelle cette propriété et on n'a pas à la supposer).

[SinusSlide]

Merci bcq, je trouve du coup que ca manque bcq de précisions dans mon bouquin (objectif prepa math Hachette ).. Pour toutes les pptés des Intégrales (linéarité, chasles, positivité, valeur absolue), les seules conditions sont la continuité des fcts sur l'intervalle.. il ne font pas mention de l'existence de la limite de la somme de riemann et donc de l'intégrale.. c ptetre sous jacent mais ca me parait important de le rappeler..
Du coup pour mon exercice,
On considere la suite (Un) definie pour tout n € N , Un=Int[0,1]x^n / (x^2+x+1) dx
Montrer que (Un) est decroissante.

Un+1 - Un = Int[0,1] x^n (x-1) / (x^2+x+1) dx
fn(x) est du signe (x-1) sur [0,1] donc négative mais je peux pas dire que L'int est négative tant que j'ai pas démontré si l'Int existe ce qui revient à la calculer ce qui semble impossible..
Il faut donc plutot que j'utilise ta proposition 2 f<g puis passage à l'int, c ca ?

[SinusSlide]

J'ai relis ce que tu m'as dit parce que je crois que je m'emmele les pinceaux

Tu as dis

La définition de l'intégrale est un passage à la limite sur les sommes de Riemann, cette limite peut donc exister ou ne pas exister. Comme conséquence de cette définition, on peut citer: 1) Si f est continue sur [a,b], alors l'intégrale existe.

Puis

Remarque: Tu as précisé que g continue sur , et tu as supposé que l'intégrale de g sur[a,b] existe (c'est que j'ai compris en te lisant,) l'existence de l'intégrale de g sur[a,b] provient alors de 1) ( on rappelle cette propriété et on n'a pas à la supposer).

Est ce que cela veut dire que pour une fct continue sur son Domaine, son intégrale (bornes dans le domaine) est DEFINIE mais que l'intégrale peut ne pas exister, c'est à dire que la limite de la somme de Riemann n'existe pas ?

Sinon je ne comprends pas pourquoi tu as dit non à

Autre question Par rapport au contraire de la positivité d'une intégrale: Si f est continue et Intégrale existe
Mais oui à

Mais si on a g(x) <ou= 0 continue et definie sur Dg, a<b € Dg et son Int existe

Désolé de tembeter..

[deltab]

Bonsoir

SinusSlide
]J'ai relis ce que tu m'as dit parce que je crois que je m'emmele les pinceaux

Tu as dis

???????

Puis



(A) Est ce que cela veut dire que pour une fct continue sur son Domaine, son intégrale (bornes dans le domaine) est DEFINIE mais que l'intégrale peut ne pas exister, c'est à dire que la limite de la somme de Riemann n'existe pas ?

(B) Sinon je ne comprends pas pourquoi tu as dit non à
??????
Jai oublié mais on supposait bien sur que a,b dans Df.
f continue sur [a,b] => Intégrale existe
Mais oui à
???????

Désolé de tembeter..

Il a des passages qui n'apparaissent plus dans ton message, problème de balises QUOTE imbriquées?

Pour ce type d'exercice, on prend en général pour Df un intervalle fermé borné.
Dans le cas contraire, on étudie l'intégrale \int_a^b f(x)dx où [a;b] est un intervalle fermé borné de Df. Si f est continue sur Df , l'intégrale définie \int_a^b f(x)dx où [a;b] est un intervalle fermé borné de Df, existe , en particulier si Df=[a;b] (c'est un théorème, voir les conséquences (donc des théorèmes) de la définition que j'avais données en particulier la conséquence 1)).
Tu as donc la réponse pour (A) où du moins je l'espère.
Pour (B), je viens de me relire, mon "non" était la réponse seulement à "le calcul intégral est tjrs un calcul d'aires"


Pour le nouvel exercice, voir post suivant.

[deltab]

Bonsoir

On considere la suite (Un) definie pour tout n € N , Un=Int[0,1]x^n / (x^2+x+1) dx
Montrer que (Un) est decroissante.

Un+1 - Un = Int[0,1] x^n (x-1) / (x^2+x+1) dx
fn(x) est du signe (x-1) sur [0,1] donc négative , mais je peux pas dire que L'int est négative

Tu as posé ici et donc et tu as dit que sur [0,1], je me demande pourquoi tu as dit ensuite "mais je peux pas dire que L'int est négative", mais SI , c'est un corollaire de la conséquence 2) avec .

Quel est le signe de ? et la conclusion qu'on peut tirer?

Est-il nécessaire de calculer l'intégrale ?
Essaies de trouver une majoration de la fonction par une fonction dont l'intégrale est simple à calculer.

[deltab]

Bonsoir

mais SI

Ici le "SI" est lié à mais (au sens négation de ce qui précéde, et non pas une condition sur ce qui suit.

Il faut plutôt lire:

-----je me demande pourquoi tu as dit ensuite "mais je peux pas dire que L'int est négative", mais SI. (fin de phase et retour à la ligne)

La relation , est un corollaire de la conséquence 2) avec .

[SinusSlide]

Salut,

Bien que tu n'as pas pu voir les citations, tu as qd meme clairement repondu à mes questions donc c'est bon pour moi.
Qd à mon "mais je peux pas dire que L'int est négative" , il venait de l'incompréhension de ton NON plus haut dans le sujet mais tu as ensuite dit dit que ce NON etait une reponse uniquement pour le calcul d'aires donc pour moi, tout est clair maintenant.

Qd à l'exercice , j'ai réussi, je pense. Un+1-Un est négatif donc Un décroissante.
J'ai encadré Un sur [0,1] par 1/(3(n+1)) et 1/(n+1) et la suite converge vers 0.

Merci bcq deltab !