exo 1 :
soit f : IR------->IR une fonction continue satisfaisant f(x+y)=f(x)+f(y) pour tous x,y IR .soit x IR un réel arbitraire .
1.Montrer que f(ax)=af(x) pour tout a IR et conclure ?
2.Donner alors la forme de f(x) pour tout x IR
exo2 :
soient E,F,G des espaces vectoriels sur IK et soient f: E---->F et g: F------->G des applications linéaires .
1.Montrer que Im(gof) est inclu dans Im(g) et ker(f) est inclu kerf(gof).
2.En déduire que si f est endomorphisme de E .alors la suite (Im(f^k) "indice k" est décroissante et la suite (ker(f^k)"indice k" est croissante (pour l'inclusion )
Important !!!
4 messages
- Page 1 sur 1
Salut !
Pour le premier, tu peux t'en sortir avec un argument de densité. Pour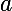 dans
dans  ça marche ( récurrence ). Ensuite dans
ça marche ( récurrence ). Ensuite dans  y a pas de problèmes ( remarquer que si
y a pas de problèmes ( remarquer que si  alors
alors  et appliquer ce qui précède ). Dans
et appliquer ce qui précède ). Dans  aussi y a pas de soucis. Et enfin tu conclus avec la densité de
aussi y a pas de soucis. Et enfin tu conclus avec la densité de  dans
dans 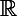 . Et ensuite pour la deuxième question, appliquer ce qui précède pour
. Et ensuite pour la deuxième question, appliquer ce qui précède pour 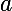 quelconque et pour
quelconque et pour  , que remarques-tu ? Qu'en est-il de la réciproque ?
, que remarques-tu ? Qu'en est-il de la réciproque ?
Pour le deuxième, généralement pour montrer une inclusion , on prend un élément de
, on prend un élément de 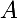 ( qu'on suppose non vide, car sinon l'inclusion est triviale ) et on regarde s'il est dans
( qu'on suppose non vide, car sinon l'inclusion est triviale ) et on regarde s'il est dans 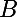 . Comment traduirais-tu
. Comment traduirais-tu ) ?
?
Note de modération : éviter les titres hors-charte. D'ailleurs c'est même écrit en rouge dans le formulaire d'envoi : "Pas de "Urgent", de "Vite" , de "Aidez moi", "DM pour demain",...".
Pour le premier, tu peux t'en sortir avec un argument de densité. Pour
Pour le deuxième, généralement pour montrer une inclusion
Note de modération : éviter les titres hors-charte. D'ailleurs c'est même écrit en rouge dans le formulaire d'envoi : "Pas de "Urgent", de "Vite" , de "Aidez moi", "DM pour demain",...".
Salut;
Si on veut éviter l'utilisation de la densité, on peut faire l'exercice 1 en utilisant le concept de primitive d'une fonction continue sur un intervalle de .
.
Soit une telle application et
une telle application et  une primitive de
une primitive de  sur
sur 
1) Prouver que :-2F(2x)+F(x)-xf(x)=0)
2) En déduire que est derivable sur chacun des intervalles
est derivable sur chacun des intervalles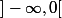 et
et 
3) Conclure (on pourra prouver ar exemple que la fonction est constante sur tout intervalle de
est constante sur tout intervalle de 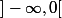 et
et  . )
. )
Si on veut éviter l'utilisation de la densité, on peut faire l'exercice 1 en utilisant le concept de primitive d'une fonction continue sur un intervalle de
Soit
1) Prouver que :
2) En déduire que
3) Conclure (on pourra prouver ar exemple que la fonction
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
