Importance sampling monte carlo
30 messages
- Page 1 sur 2 - 1, 2
Importance sampling monte carlo
J'ai question très simple que je n'arrive pas terminée
Given an importance sample (Xi,f(Xi)/g(Xi)), where the weights
wi~Poisson(f(Xi)/g(Xi)), montrons que l'estimateur i/n*somme(wi*h(xi)) est non biaisé et déduire que l'échantillon dérivé de ce mécanisme est marginalement distribué de f.
ie l'estimateur est non biaisé si E( i/n*somme(wi*h(Xi)) )=E(h(X)) je crois
...
Given an importance sample (Xi,f(Xi)/g(Xi)), where the weights
wi~Poisson(f(Xi)/g(Xi)), montrons que l'estimateur i/n*somme(wi*h(xi)) est non biaisé et déduire que l'échantillon dérivé de ce mécanisme est marginalement distribué de f.
ie l'estimateur est non biaisé si E( i/n*somme(wi*h(Xi)) )=E(h(X)) je crois
...
Importance sampling monte carlo
J'ai question très simple que je n'arrive pas terminée
Given an importance sample (Xi,f(Xi)/g(Xi)), where the weights
wi~Poisson(f(Xi)/g(Xi)), montrons que l'estimateur i/n*somme(wi*h(xi)) est non biaisé et déduire que l'échantillon dérivé de ce mécanisme est marginalement distribué de f.
ie l'estimateur est non biaisé si E( i/n*somme(wi*h(Xi)) )=E(h(X)) je crois
où les Xi sont générer à partir de g
...
Given an importance sample (Xi,f(Xi)/g(Xi)), where the weights
wi~Poisson(f(Xi)/g(Xi)), montrons que l'estimateur i/n*somme(wi*h(xi)) est non biaisé et déduire que l'échantillon dérivé de ce mécanisme est marginalement distribué de f.
ie l'estimateur est non biaisé si E( i/n*somme(wi*h(Xi)) )=E(h(X)) je crois
où les Xi sont générer à partir de g
...
Le contexte du chapitre du livre est l'intégration de monte carlo
Plus précisément, ici c'est un exercice sur le sampling importance resampling(échantillonnage préférentiel)
La question mot pour mot est :
Given an importance sample (Xi,f(Xi)/g(Xi)), show that, if wi has a Poisson distribution, wi~Poisson(f(Xi)/g(Xi)), the estimator 1/n*somme(wi*h(xi)) is unbiaised. Deduce that the sample derived from this sampling mecanism is marginaly distributed from f.
En francais, ca donne :
Donné un échantillonnage préférentiel (Xi,f(Xi)/g(Xi)), montrez que, si wi suivent une loi de Poisson(f(Xi)/g(Xi)), l'estimateur 1/n*somme(wi*h(xi)) est non biaisé. En déduire que l'échantillon provenant de ce mécanisme d'échantillonnage est marginalement distribué de f.
Notation Ef est l'espérance prise sous la densité f
et h est une fonction quelconque
On veut donc montrer que Eg(1/n*somme(wi*h(xi)))=Ef(h(X)) tel que au départ, les Xi sont générés à partir de g
On a donc E(1/n*somme(wi*h(Xi)))=1/n*somme(E(wi*h(Xi))) mais après je sais pas trop quoi faire, je sais par contre que E(wi)=f(Xi)/g(Xi) et de plus une des propriétés de l'échantillonage préférentiel est
Eg(f(Xi)*h(Xi)/g(Xi))=Ef(h(Xi)) où la seule condition sur g est que support(f) inclus dans support(g)
...
De plus, d'habitude, quand on parle des wi, ce sont les poids f(Xi)/n*g(Xi) qui sont normalisés, soit wi=(f(Xi)/g(Xi))/somme(f(Xi)/g(Xi))
Plus précisément, ici c'est un exercice sur le sampling importance resampling(échantillonnage préférentiel)
La question mot pour mot est :
Given an importance sample (Xi,f(Xi)/g(Xi)), show that, if wi has a Poisson distribution, wi~Poisson(f(Xi)/g(Xi)), the estimator 1/n*somme(wi*h(xi)) is unbiaised. Deduce that the sample derived from this sampling mecanism is marginaly distributed from f.
En francais, ca donne :
Donné un échantillonnage préférentiel (Xi,f(Xi)/g(Xi)), montrez que, si wi suivent une loi de Poisson(f(Xi)/g(Xi)), l'estimateur 1/n*somme(wi*h(xi)) est non biaisé. En déduire que l'échantillon provenant de ce mécanisme d'échantillonnage est marginalement distribué de f.
Notation Ef est l'espérance prise sous la densité f
et h est une fonction quelconque
On veut donc montrer que Eg(1/n*somme(wi*h(xi)))=Ef(h(X)) tel que au départ, les Xi sont générés à partir de g
On a donc E(1/n*somme(wi*h(Xi)))=1/n*somme(E(wi*h(Xi))) mais après je sais pas trop quoi faire, je sais par contre que E(wi)=f(Xi)/g(Xi) et de plus une des propriétés de l'échantillonage préférentiel est
Eg(f(Xi)*h(Xi)/g(Xi))=Ef(h(Xi)) où la seule condition sur g est que support(f) inclus dans support(g)
...
De plus, d'habitude, quand on parle des wi, ce sont les poids f(Xi)/n*g(Xi) qui sont normalisés, soit wi=(f(Xi)/g(Xi))/somme(f(Xi)/g(Xi))
On n'a pas le livre sous les yeux.
ça nous aiderait si tu définissait les fonctions f, g et h.
Il faudrait aussi dire de quoi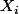 est un échantillon. Quelles sont les hypothèses.
est un échantillon. Quelles sont les hypothèses.
ta traduction de "marginaly distributed from f" est louche. Il veut peut être dire est une loi marginale dérivée de f.
ps : pas de double post, j'ai fusionné.
ça nous aiderait si tu définissait les fonctions f, g et h.
Il faudrait aussi dire de quoi
ta traduction de "marginaly distributed from f" est louche. Il veut peut être dire est une loi marginale dérivée de f.
ps : pas de double post, j'ai fusionné.
le livre c'est introducing R monte carlo statistical methods, c'est le premier exercice quand il rentre dans la section de sampling importance resampling
ce qu'on veut au fond quand on veut estimer une integrale, c'est par exemple integrale de h(x)f(x)dx où h est une fonction standard, par exemple une indicatrice qui restreint alors le domaine d'integration de la densité f
on a donc une densité f qui est compliquée et donc, au lieu de générer des Xi à partir de f pour évaluer l'integrale, on génère les Xi à partir d'une densité instrumentale g
Donc en résumé si on veut estimer l'integrale de h(x)f(x)dx = Ef(h(X))
On prend l'estimateur 1/n*somme(h(Xi))
sauf que le probleme dans l'importance sampling, c'est que générer des Xi de f est trop compliqué, donc on génère des Xi de g et on veut estimer
integrale de h(x)f(x)g(x)/g(x) = Eg(h(X)*f(X)/g(X))
On prend alors l'estimateur 1/n*somme(h(Xi)*f(Xi)/g(Xi))
EDIT: est-ce que c ok comme ca?
ce qu'on veut au fond quand on veut estimer une integrale, c'est par exemple integrale de h(x)f(x)dx où h est une fonction standard, par exemple une indicatrice qui restreint alors le domaine d'integration de la densité f
on a donc une densité f qui est compliquée et donc, au lieu de générer des Xi à partir de f pour évaluer l'integrale, on génère les Xi à partir d'une densité instrumentale g
Donc en résumé si on veut estimer l'integrale de h(x)f(x)dx = Ef(h(X))
On prend l'estimateur 1/n*somme(h(Xi))
sauf que le probleme dans l'importance sampling, c'est que générer des Xi de f est trop compliqué, donc on génère des Xi de g et on veut estimer
integrale de h(x)f(x)g(x)/g(x) = Eg(h(X)*f(X)/g(X))
On prend alors l'estimateur 1/n*somme(h(Xi)*f(Xi)/g(Xi))
EDIT: est-ce que c ok comme ca?
Oui, c'est ok.
Donc si tu prends le Eg de ton estimateur, tu retombes bien sur ce que tu veux estimer.
Et si h=1 Eg(f(X)/g(X))=1.
Il y a pas mal de réf sur internet pour comprendre la méthode qui sont assez accessibles.
Je ne suis pas certain d'avoir bien compris le "marginaly distributed".
Quant au biais, sur wikipédia ils en parlent un peu sur wikipedia (art échantillon préférentiel), mais ce n'est pas très clair.
Mes souvenirs de la méthode de montécarlo manquent de précision...
Donc si tu prends le Eg de ton estimateur, tu retombes bien sur ce que tu veux estimer.
Et si h=1 Eg(f(X)/g(X))=1.
Il y a pas mal de réf sur internet pour comprendre la méthode qui sont assez accessibles.
Je ne suis pas certain d'avoir bien compris le "marginaly distributed".
Quant au biais, sur wikipédia ils en parlent un peu sur wikipedia (art échantillon préférentiel), mais ce n'est pas très clair.
Mes souvenirs de la méthode de montécarlo manquent de précision...
Oui avant de voir ce message j'ai fait quelque chose :
les détails sont:
Eg(i/n*somme(wi*h(Xi)))=1/n*somme(Eg(wi*h(Xi))) par linéarité
=1/n*somme(integrale(wi*h(xi)*g(xi)) sur Dom(g))
=1/n*somme(integrale(f(xi)/g(xi)*h(xi)*g(xi)) sur Dom(g))
où les wi=f(xi)/g(xi) lorsque non normalisés
=1/n*somme(integrale(h(xi)*f(xi)) sur Dom(f)) car f et g ont le même support
=1/n*somme(Ef(h(Xi)))
=1/n*somme(Ef(h(X))) car les Xi~g sont iid
=Ef(h(X)) precisement ce qu<on veut estimer
Le problème, ce que je n'utilise pas l'hypothèse wi~Poisson(f(Xi)/g(Xi))
Donc, c'est sur que il y a une erreur...
Et de plus, on sait que l'hypothèse sert à la première partie de la question
Pour la deuxième partie de la question c ok, car si on a X*~Multinomiale(n,w1,...,wn) où wi=f(Xi)/(n*g(Xi))
On a que P(X*elemA)=somme(P(X*elemA et X*=Xi))
=somme(integrale(1(Xi elemA)*f(xi)/(n*g(xi))*g(xi)) sur Dom(g))
=somme(1/n*integrale(f(xi)) sur A)
=1/n*somme(integrale(f(xi)) sur A)
=integrale(f(x)) sur A car les Xi~g sont iid
donc, on a bien que X*~f, ce qu'on voulait (cette réponse est dans le livre)
les détails sont:
Eg(i/n*somme(wi*h(Xi)))=1/n*somme(Eg(wi*h(Xi))) par linéarité
=1/n*somme(integrale(wi*h(xi)*g(xi)) sur Dom(g))
=1/n*somme(integrale(f(xi)/g(xi)*h(xi)*g(xi)) sur Dom(g))
où les wi=f(xi)/g(xi) lorsque non normalisés
=1/n*somme(integrale(h(xi)*f(xi)) sur Dom(f)) car f et g ont le même support
=1/n*somme(Ef(h(Xi)))
=1/n*somme(Ef(h(X))) car les Xi~g sont iid
=Ef(h(X)) precisement ce qu<on veut estimer
Le problème, ce que je n'utilise pas l'hypothèse wi~Poisson(f(Xi)/g(Xi))
Donc, c'est sur que il y a une erreur...
Et de plus, on sait que l'hypothèse sert à la première partie de la question
Pour la deuxième partie de la question c ok, car si on a X*~Multinomiale(n,w1,...,wn) où wi=f(Xi)/(n*g(Xi))
On a que P(X*elemA)=somme(P(X*elemA et X*=Xi))
=somme(integrale(1(Xi elemA)*f(xi)/(n*g(xi))*g(xi)) sur Dom(g))
=somme(1/n*integrale(f(xi)) sur A)
=1/n*somme(integrale(f(xi)) sur A)
=integrale(f(x)) sur A car les Xi~g sont iid
donc, on a bien que X*~f, ce qu'on voulait (cette réponse est dans le livre)
Ouimet21 a écrit:Oui avant de voir ce message j'ai fait quelque chose :
les détails sont:
Eg(i/n*somme(wi*h(Xi)))=1/n*somme(Eg(wi*h(Xi))) par linéarité
=1/n*somme(integrale(wi*h(xi)*g(xi)) sur Dom(g))
Il y a un pb ici, au moins de rédaction. wi est une loi conditionné par Xi et non une fonction de Xi
Par contre E (wi h(Xi)| Xi) = f(Xi)h(Xi)/g(Xi) (espérance conditionnée à Xi)
Et on peut prendre l'espérance classique. (l'esp de l'esp conditionnelle est toujours égale à l'espérance)
Là on utilise le fait que la loi est de poisson car on utilise le fait que son espérance est égale à son paramètre.
Excuse moi mais tu n'a pas répondu, qu'est que l'auteur estime avec cette estimateur dans ce passage? je suis quasiment certain que ce qu'il essaye d'estimer contient ce fameux h.
C'est peut être évident pour toi par ce que tu a lu le livre en question jusqu'à ce passage, mais pas nous. Alors tant que tu replace pas complétement le problème, on ne peut t'aider plus.
Dire que c'est le premier exercice ne suffit pas, je ne vais pas allé acheter le livre juste pur comprendre ce que tu as a dire.
EDIT] désolé j'ai pas lu ton deuxieme paragraphe, et comme tu n'utilise pas les formule latex, ct pas immédiat à la lecture rapide.
donc ton quelque chose du genre contient bien le h.
C 'est etrange comme utilisation du monte carlo, pourquoi l'auteur n'applique t'il pas le principe à f(x)h(x) plutot qu'à f tout seule?
Et pourquoi une loi de poisson pour les wi, ça marche tout autant si ce n'est mieux avec le rapport f/g directement.
Pour les calculs je pencherai pour l'utilisation des espérances conditionnels et de leur définition, mais mes souvenir sur ce sujet sont bien vieux.
C'est peut être évident pour toi par ce que tu a lu le livre en question jusqu'à ce passage, mais pas nous. Alors tant que tu replace pas complétement le problème, on ne peut t'aider plus.
Dire que c'est le premier exercice ne suffit pas, je ne vais pas allé acheter le livre juste pur comprendre ce que tu as a dire.
EDIT] désolé j'ai pas lu ton deuxieme paragraphe, et comme tu n'utilise pas les formule latex, ct pas immédiat à la lecture rapide.
donc ton quelque chose du genre contient bien le h.
C 'est etrange comme utilisation du monte carlo, pourquoi l'auteur n'applique t'il pas le principe à f(x)h(x) plutot qu'à f tout seule?
Et pourquoi une loi de poisson pour les wi, ça marche tout autant si ce n'est mieux avec le rapport f/g directement.
Pour les calculs je pencherai pour l'utilisation des espérances conditionnels et de leur définition, mais mes souvenir sur ce sujet sont bien vieux.
Ouimet21 a écrit:E (wi h(Xi)| Xi) = f(Xi)h(Xi)/g(Xi)
Mais comment on justifie cette ligne, et oui tu as raison wi ne sont pas fonction de Xi
Tu connais la loi conditionnelle de wi par rapport à Xi. L'espérance pour la loi conditionnelle donne l'espérance conditionnelle.
Il faut faire attention en général avec les espérances conditionnelles pour des va continues mais ça ça reste vrai.
Finrod a écrit:Tu connais la loi conditionnelle de wi par rapport à Xi. L'espérance pour la loi conditionnelle donne l'espérance conditionnelle.
Il faut faire attention en général avec les espérances conditionnelles pour des va continues mais ça ça reste vrai.
Oui mais c'est le h(Xi) qui me dérange, on fait quoi avec, il sort pas de l'espérance...
Et même, si on admet ton raisonnement, on se retrouve avec
1/n*somme(f(Xi)*h(Xi)/g(Xi))
et on veut Ef(h(X)) à la fin
donc, encore la je voit pas le step, ce qu'on peut dire c'est que
1/n*somme(f(Xi)*h(Xi)/g(Xi)) estime Ef(h(X))
c'est-à-dire, 1/n*somme(f(Xi)*h(Xi)/g(Xi)) --> Ef(h(X)) pour n-->infini
mais on veut une égalité, alors, si tu peux développé les calculs, ce serait très apprécié
merci
D'accord c'est plus claire,
il est normal que tu n'y arrive pas directement avec h, en faite de façon ultra rigoureuse il faut le démontré pour les fonctions indicatrice des boreliens de l'espace des épreuves (ou l'on retombe sur la définition de P(Wi ds B), puis par linéarité sur les fonctions étagées positives (combinaison linéaire des indicatrices), après on étend par convergence monotone aux limites des suite de telles fonctions.
Par contre la fonction h devrait être soumise à la condition d'être positive (peut-tu vérifier)?
bon pour me décrasser un peu je me suis plongé dans les calculs; désolé si je répète ce qui vous avez déjà dis.
L'auteur est donc soumis au problème de calculer l'intégrale suivante, il a la judicieuse idée d'utiliser la méthode de monté carlo :
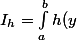 f(y) dy}=\int_a^b{h(y) dP_{\bf{Y}}(y)} = \bf{E}[h(\bf{Y})]})
où Y suit la loi de densité f. Or f est une densité difficile à simuler, il a donc recours à une densité auxiliaire plus simple g. Notons X la v.a. issue de cette nouvelle densité :
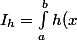 \frac{f(x)}{g(x)} g(x) dx} = \bf{E}[h(\bf{X}) w(\bf{X})]})
on note w(.)=f(.)/g(.) l'importance de la nouvelle distribution (pour l'instant j'utilise l'importance brut pour avoir un élément de comparaison)
pour estimer cette dernière espérance il utilise un échantillonnage_{i=1..n}) de n simulations successifs et indépendants de la v.a. X.
de n simulations successifs et indépendants de la v.a. X.
avec pour estimateur la moyenne empirique : w(\bf{X}_i)}})
cette estimateur est sans biais, en effet :
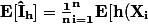 w(\bf{X}_i)]} = \bf{E}[h(\bf{X}) w(\bf{X})]\ \frac{1}{n}\Bigsum_{i=1}^{n}{1} = I_h})
Et sa variance vaut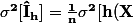 w(\bf{X})] = \frac{1}{n}\(\bf{E}[h(\bf{X})^2 w(\bf{X})^2]-I_h^2\)})
Toujours pas satisfait des résultats, il compte bien améliorer son estimateur, en jouant sur l'importance w de la densité auxiliaire g. Il espère ainsi simplifier les calculs (les wi ne sont que des simples entiers pour une loi discrete), mais qu'advient-il de la variance.
Il fait donc une deuxième étape de simulation durant laquelle il simule un échantillonnage de l'importance_{i=1..n}) , où pour tout i
, où pour tout i )) avec
avec ) la loi de poisson de paramètre
la loi de poisson de paramètre 
Aparté sur les notations :
Pour être plus juste je devrais plutôt noter les réalisations des v.a.
les réalisations des v.a. 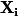 , mais comme vous l'aurez compris, je parle d'échantillonnage en tant qu'élément aléatoire et pas simplement de la donnée d'une réalisation particulière de cette échantillon. C'est comme l'estimateur
, mais comme vous l'aurez compris, je parle d'échantillonnage en tant qu'élément aléatoire et pas simplement de la donnée d'une réalisation particulière de cette échantillon. C'est comme l'estimateur 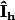 , qui dans mon texte est un élément aléatoire qui se réalise lors de la simulation d'un échantillon
, qui dans mon texte est un élément aléatoire qui se réalise lors de la simulation d'un échantillon _{i=1..n}) en une estimation de
en une estimation de 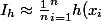w(x_i)})
Fin de l'aparté.
Il obtient donc un nouvelle estimateur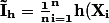 \bf{W}_i}})
Cette estimateur aussi est sans biais :
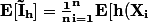 \bf{W}_i]}})
on calcul les espérances dans la somme avec les espérances conditionnées à X_i (donc à X par indépendance) :
 \bf{W}_i]=\bf{E}[\bf{E}[h(\bf{X}_i) \bf{W}_i|\bf{X}_i]]}=\bf{E}[h(\bf{X}_i)E[\bf{W}_i|\bf{X}_i]])
or justement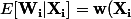) en tant qu'espérance d'une loi de poisson.
en tant qu'espérance d'une loi de poisson.
Finalement on retombe bien sur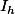 avec les même calcul que le précédent estimateur. (on peut revenir, pour justifier les transitions, à l'écriture sous forme intégrale mais c'est gâcher l'utilité et la simplicité de la notation E[.])
avec les même calcul que le précédent estimateur. (on peut revenir, pour justifier les transitions, à l'écriture sous forme intégrale mais c'est gâcher l'utilité et la simplicité de la notation E[.])
Quand à la variance de ce nouvel estimateur on trouve (il faut calculer le moment d'ordre 2 de la loi de poisson) :
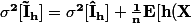^2 w(\bf{X})]})
Il a donc perdu en précision de façon significative en voulant simplifier ces calcul (qu'il a mis d'ailleurs deux fois plus de temps à réaliser). Il avait tout autant intéret à chercher une autre densité g. L'élément bloquant dans la méthode de monté carlo est la simulation de l'echantillon et pas comme au temps des machine 8 ou 16 bit la multiplication des flottants.
Avec des registres internes de 64 bits la précision est suffisante pour la grande majorité des applications numériques, et l'instabilité due aux erreurs d'approximation des réels moins pertinente.
il est normal que tu n'y arrive pas directement avec h, en faite de façon ultra rigoureuse il faut le démontré pour les fonctions indicatrice des boreliens de l'espace des épreuves (ou l'on retombe sur la définition de P(Wi ds B), puis par linéarité sur les fonctions étagées positives (combinaison linéaire des indicatrices), après on étend par convergence monotone aux limites des suite de telles fonctions.
Par contre la fonction h devrait être soumise à la condition d'être positive (peut-tu vérifier)?
bon pour me décrasser un peu je me suis plongé dans les calculs; désolé si je répète ce qui vous avez déjà dis.
L'auteur est donc soumis au problème de calculer l'intégrale suivante, il a la judicieuse idée d'utiliser la méthode de monté carlo :
où Y suit la loi de densité f. Or f est une densité difficile à simuler, il a donc recours à une densité auxiliaire plus simple g. Notons X la v.a. issue de cette nouvelle densité :
on note w(.)=f(.)/g(.) l'importance de la nouvelle distribution (pour l'instant j'utilise l'importance brut pour avoir un élément de comparaison)
pour estimer cette dernière espérance il utilise un échantillonnage
avec pour estimateur la moyenne empirique :
cette estimateur est sans biais, en effet :
Et sa variance vaut
Toujours pas satisfait des résultats, il compte bien améliorer son estimateur, en jouant sur l'importance w de la densité auxiliaire g. Il espère ainsi simplifier les calculs (les wi ne sont que des simples entiers pour une loi discrete), mais qu'advient-il de la variance.
Il fait donc une deuxième étape de simulation durant laquelle il simule un échantillonnage de l'importance
Aparté sur les notations :
Pour être plus juste je devrais plutôt noter
Fin de l'aparté.
Il obtient donc un nouvelle estimateur
Cette estimateur aussi est sans biais :
on calcul les espérances dans la somme avec les espérances conditionnées à X_i (donc à X par indépendance) :
or justement
Finalement on retombe bien sur
Quand à la variance de ce nouvel estimateur on trouve (il faut calculer le moment d'ordre 2 de la loi de poisson) :
Il a donc perdu en précision de façon significative en voulant simplifier ces calcul (qu'il a mis d'ailleurs deux fois plus de temps à réaliser). Il avait tout autant intéret à chercher une autre densité g. L'élément bloquant dans la méthode de monté carlo est la simulation de l'echantillon et pas comme au temps des machine 8 ou 16 bit la multiplication des flottants.
Avec des registres internes de 64 bits la précision est suffisante pour la grande majorité des applications numériques, et l'instabilité due aux erreurs d'approximation des réels moins pertinente.
Wow, chapeau, ton explication est un chef d'oeuvre,
mais, je ne suis pas sûr de la justification d'une des égalités
Est-ce qu'on peut dire E(E(h(Xi)*Wi|Xi))=E(h(Xi)*E(Wi|Xi))
car h(Xi) est constant?, c'est-à-dire qu'il faudrait écrire h(xi) car on a Xi=xi comme condition?
Pour ce qui est de ton premier paragraphe, je ne comprends absolument rien, je n'en suis qu'à ma première année d'université...
De plus, pour h, la condition selon laquelle h devrait être positive n'est pas mentionnée, en fait h(X)=X^3, ie si on veut évaluer Ef(X^3), soit le 3e moment pour une densité f (compliquée), on a que h n'est pas positive si X<0, par exemple, on peut tout simplement penser à une loi normale, 1 fois sur deux h(X)<0.
mais, je ne suis pas sûr de la justification d'une des égalités
Est-ce qu'on peut dire E(E(h(Xi)*Wi|Xi))=E(h(Xi)*E(Wi|Xi))
car h(Xi) est constant?, c'est-à-dire qu'il faudrait écrire h(xi) car on a Xi=xi comme condition?
Pour ce qui est de ton premier paragraphe, je ne comprends absolument rien, je n'en suis qu'à ma première année d'université...
De plus, pour h, la condition selon laquelle h devrait être positive n'est pas mentionnée, en fait h(X)=X^3, ie si on veut évaluer Ef(X^3), soit le 3e moment pour une densité f (compliquée), on a que h n'est pas positive si X<0, par exemple, on peut tout simplement penser à une loi normale, 1 fois sur deux h(X)<0.
oui justement elle est "constante" dans la mesure de la conditionnel Xi. Pour justifier clairement il faut retourner à l'intégrale (ou la somme pour les lois discrètes). Ne pas oublier aussi qu'une espérance conditionnel est une autre v.a. et non une valeur.
|X=x]=\phi(x)) (là c'est une vrai constante)
(là c'est une vrai constante)
puis on compose à droite avec la v.a. X (en tant qu'application de l'univers des éventualités dans l'espace des événements)
on obtient donc bien la v.a.)
puis on compose à droite avec la v.a. X (en tant qu'application de l'univers des éventualités dans l'espace des événements)
on obtient donc bien la v.a.
Ouimet21 a écrit:Pour ce qui est de ton premier paragraphe, je ne comprends absolument rien, je n'en suis qu'à ma première année d'université...
C'était surtout pour préciser, que les "calculs" que j'utilise ne sont en faite que des notations, la justification rigoureuse et mathématique consiste à prouver le résultat pour des familles de fonctions h d'abord simple puis d'utiliser des principes de passage à la limite (théorème de convergence monotone et dominé)
Un peu comme lors de la construction des integrales de riemann et lebesgue.
les notions sont abordés en master, la première année d'université c'est un peu juste. mais si tu arrive à comprendre le principe c'est l'essentiel, et un très bon départ pour toi.
30 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
