A²=0 implique rg(A)<=1 ?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zobobo
- Membre Naturel
- Messages: 72
- Enregistré le: 04 Nov 2007, 21:03
-
 par zobobo » 16 Juin 2008, 08:17
par zobobo » 16 Juin 2008, 08:17
Bonjour
A t on A²=0 implique rg(A)<=1 ?
Merci
-
Cyril Mar
- Membre Naturel
- Messages: 61
- Enregistré le: 22 Mai 2008, 23:40
-
 par Cyril Mar » 16 Juin 2008, 08:28
par Cyril Mar » 16 Juin 2008, 08:28
Qu'est-ce que A ? Une matrice ? Un espace vectoriel (famille de vecteurs) ? Etc.
Je veux dire précise ton énoncé.
-
zobobo
- Membre Naturel
- Messages: 72
- Enregistré le: 04 Nov 2007, 21:03
-
 par zobobo » 16 Juin 2008, 10:08
par zobobo » 16 Juin 2008, 10:08
A est une matrice
-
sclormu
- Membre Naturel
- Messages: 36
- Enregistré le: 16 Juin 2008, 10:23
-
 par sclormu » 16 Juin 2008, 10:35
par sclormu » 16 Juin 2008, 10:35
(Yope.)
C'est faux. Considère une matrice avec des blocs
0 1
0 0
sur la diagonale.
Essaie d'appliquer le théorème du rang, cela te donnera une inégalité un peu plus large (mais vraie).
-
zobobo
- Membre Naturel
- Messages: 72
- Enregistré le: 04 Nov 2007, 21:03
-
 par zobobo » 16 Juin 2008, 11:40
par zobobo » 16 Juin 2008, 11:40
Si A non nulle
on a 1<=rg(A)<=n-1
ms n'y a t il pas d'encadrement plus précis, pas forcément dans le cas p=2 mais ds le cas général où A^p=0 ?
-
sclormu
- Membre Naturel
- Messages: 36
- Enregistré le: 16 Juin 2008, 10:23
-
 par sclormu » 16 Juin 2008, 12:24
par sclormu » 16 Juin 2008, 12:24
Interprete
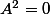
en termes d'image et de noyau.
-
zobobo
- Membre Naturel
- Messages: 72
- Enregistré le: 04 Nov 2007, 21:03
-
 par zobobo » 16 Juin 2008, 13:33
par zobobo » 16 Juin 2008, 13:33
ImA c Ker A donc rg(A)<=n/2
Mais plus generalement pour une mztricef nilpotente d'indice p peut - on avoir un encadrement plus précis que 1<=rg(A)<=n-1 ?
-
sclormu
- Membre Naturel
- Messages: 36
- Enregistré le: 16 Juin 2008, 10:23
-
 par sclormu » 16 Juin 2008, 16:52
par sclormu » 16 Juin 2008, 16:52
Si elle est nilpotente d'indice p, tu peux trouver

tel que les

soient libres pour

(au boulot).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
