OK, donc c'est bien ce que j'avais compris et c'est bien ce qu'il faut chercher.
L'image d'un (sous-)espace vectoriel par une application linéaire est un espace vectoriel dont la dimension est inférieure ou égale à celle de l'espace de départ. Donc dire que l'image d'un plan est "incluse dans une droite", c'est exactement dire que l'image du plan est une droite, ou l'image du plan est le vecteur nul.
De façon rigoureuse, il faudrait vérifier que
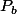
est bien un plan vectoriel : l'énoncé le suggère, mais existerait-il par hasard une valeur de

qui ferait que
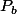
soit une droite ? (en fait non, mais ça vaudrait quand même le coup de le vérifier : comment vérifie-t-on que le système
)
est libre ou lié ?)
Par suite :
1) Peut-on dire que
)
est une base de
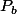
?
2) Que peut-on dire de l'image
d'une base de
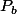
au regard de l'image de
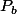
?
3) Dans quel cas l'image de
)
constitue-t-il un système libre ? Un système lié ?
4) Conclusion : à quelle condition (sur

évidemment)l'image de
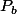
est-il une droite ? le vecteur nul ?
(Les 3 premières questions ne nécessitent aucun calcul, aucune formule, ce sont simplement des "réponses d'application des définitions du cours", une réponse par une phrase en français est requise ici. La quatrième question met en œuvre les réponses précédentes).
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
