Image et Noyau
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 09 Juin 2010, 18:35
par Finrod » 09 Juin 2010, 18:35
Oui c'est bon.
ma connexion avait planté, j'ai mis un peu de temps à répondre.
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 09 Juin 2010, 20:22
par Near » 09 Juin 2010, 20:22
Finrod a écrit:Oui c'est bon.
ma connexion avait planté, j'ai mis un peu de temps à répondre.
merci beaucoup :we:
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 10 Juin 2010, 14:35
par Near » 10 Juin 2010, 14:35
Re-salut
j'ai une autre question :zen:
comment trouver la dimension de Imf ?
on a

donc

est-ce juste ?
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 10 Juin 2010, 14:50
par miikou » 10 Juin 2010, 14:50
en effet on a bien la relation miracle n+1-2 = n-1 :++:
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 10 Juin 2010, 14:57
par Near » 10 Juin 2010, 14:57
miikou a écrit:en effet on a bien la relation miracle n+1-2 = n-1 :++:
merci :we: ,ma dernière question :zen:
déterminer une base de

.
je trouve
)
,c'est bon :we:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Juin 2010, 15:02
par Doraki » 10 Juin 2010, 15:02
Tu connais un polynôme P tel que f(P) = 1 ?
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 10 Juin 2010, 15:04
par Near » 10 Juin 2010, 15:04
Doraki a écrit:Tu connais un polynôme P tel que f(P) = 1 ?
Salut "Doraki" :zen:
où est mon erreur :mur:
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 10 Juin 2010, 15:07
par miikou » 10 Juin 2010, 15:07
l'image dune base est une base non ?
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 10 Juin 2010, 15:08
par miikou » 10 Juin 2010, 15:08
calcul tout les f(p)
ou p est un element de la base de Rn[x] et tu verra
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 10 Juin 2010, 15:18
par Near » 10 Juin 2010, 15:18
ok,j'ai trouvé
=(1-n)X^n)
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Juin 2010, 15:20
par Doraki » 10 Juin 2010, 15:20
T'avais pas dit à un moment que f(X) = 0 ?
On a bien f(P) = X*P" ?
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 10 Juin 2010, 15:23
par Near » 10 Juin 2010, 15:23
Doraki a écrit:T'avais pas dit à un moment que f(X) = 0 ?
On a bien f(P) = X*P" ?
où ça ? je sais pas :hum:
sinon ce que j'ai écrit maintenant est-il faux ? :we:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Juin 2010, 15:27
par Doraki » 10 Juin 2010, 15:27
Le problème c'est que au début de ce sujet t'as f(P) = xP", mais là tu parles de l'autre sujet, où t'as f(P) = P - xP'.
Si c'est le premier cas, bah j'voulais te faire remarquer que 1 n'est pas dans l'image de f.
De toutes façons, dans les deux cas, f(X^n) est un polynôme de degré (n-1) ou n, donc l'image de f ne peut pas être Vect(1,X,...,X^(n-2)) = R(n-2)[X].
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 10 Juin 2010, 15:38
par Near » 10 Juin 2010, 15:38
Doraki a écrit:Le problème c'est que au début de ce sujet t'as f(P) = xP", mais là tu parles de l'autre sujet, où t'as f(P) = P - xP'.
Si c'est le premier cas, bah j'voulais te faire remarquer que 1 n'est pas dans l'image de f.
De toutes façons, dans les deux cas, f(X^n) est un polynôme de degré (n-1) ou n, donc l'image de f ne peut pas être Vect(1,X,...,X^(n-2)) = R(n-2)[X].
oui "Doraki" c'est ma faute désolé on a bien
=xP")
:hum:
=nX^n,\forall n\geq 2)
,donc
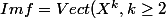)
,non ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Juin 2010, 16:05
par Doraki » 10 Juin 2010, 16:05
nan, chez moi, f(X²) ça fait pas 2X², mais ça fait 2X.
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 10 Juin 2010, 16:46
par Near » 10 Juin 2010, 16:46
Doraki a écrit:nan, chez moi, f(X²) ça fait pas 2X², mais ça fait 2X.
ma dernière tentative,
=n(n-1)X^{n-1},n\geq 2)
)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Juin 2010, 16:59
par Ben314 » 10 Juin 2010, 16:59
Salut,
Pour voir si c'est cohérent, tu n'as qu'a regarder quelle est la dimension ton Im(f) et de vérifier que c'est cohérent avec la dimension de Ker(f) que tu as trouvé...
P.S. : tu ferait mieux d'écrire
=k(k-1)X^{k-1})
vu qu'un

, il y en a déjà un dans l'énoncé...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Near
- Membre Relatif
- Messages: 312
- Enregistré le: 10 Déc 2008, 16:42
-
 par Near » 10 Juin 2010, 17:02
par Near » 10 Juin 2010, 17:02
Ben314 a écrit:Salut,
Pour voir si c'est cohérent, tu n'as qu'a regarder quelle est la dimension ton Im(f) et de vérifier que c'est cohérent avec la dimension de Ker(f) que tu as trouvé...
je trouve que c'est juste,mé je veux que tu le vérifie aussi :zen:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Juin 2010, 17:02
par Ben314 » 10 Juin 2010, 17:02
Oui, c'est juste (mais prend k à la place de n, sinon tu vas complètement t'embrouiller...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Juin 2010, 17:04
par Doraki » 10 Juin 2010, 17:04
Ah aussi, c'est assez maladroit de réutiliser n comme une variable alors que c'est un entier censé être fixé depuis le début :
f(X^k) = k(k-1)X^(k-1), pour 0 <= k <= n, ok, et là, y'a pas d'ambiguïté.
En te lisant les gens risqueraient par exemple de croire que tu veux dire
Im f = Vect(X^1,X^2, ... , X^n). Alors que c'est pas le cas.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
=k(k-1)X^{k-1}) vu qu'un
vu qu'un  , il y en a déjà un dans l'énoncé...
, il y en a déjà un dans l'énoncé...