Les hypothèses sont importantes, car c'est faux en dimension infinie.
Par exemple, considérons
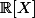
, l'espace vectoriel des polynômes à coefficients réels, et f l'application linéaire "dérivée" (on vérifie aisément que c'est une appli linéaire).
Alors
=\R[X])
car tout polynôme est la dérivée d'un (et même e plusieurs) polynômes de degré immédiatement supérieur. Donc
=Im(f))
Par contre
)
c'est l'ensemble des polynômes constants (de degré nul), et
)
c'est l'ensemble des polynômes de degré 0 ou 1, donc
\neq Ker(f))
.
En dimension finie par contre, même sans raisonner en somme des dimensions : si
c'est que la restriction de
sur
)
est un isomorphisme.
- surjectif : tout élément
)
étant dans )
, il s'écrit ))
et \in Im(f))
- injectif : considérer une base de Im(f), l'image par f de cett base est également une base de Im(f). On prend alors deux éléments de Im(f) et on dit qu'ils ont la même image par f, on arrive rapidement à une combinaison linéaire nulle de la base qui montre que les deux éléments sont égaux.
Par suite
=0)
ssi
=0)
puisque le noyau d'un isomorphisme est le singleton {0}
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
