Image essentielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Als128
- Membre Relatif
- Messages: 132
- Enregistré le: 30 Oct 2009, 12:43
-
par Als128 » 24 Déc 2009, 08:13
Bonjour,
j'ai une petite question concernant mon raisonnement pour une reponse (ça parait simple mais bon, je suis pas vraiment sur de mes raisonnements...)
L'énoncé de l'exo dit :
Pour f une fonction mesurable bornée definie sur un espace mesuré
)
on dit que le point x de
est dans l'image essentielle de f (pour m) si :
-x|0)
la question : montrer que si
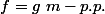
alors
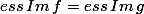
j'ai procédé par double inégalité en disant que :
-x|=|f(\omega)-g(\omega)+g(\omega)-x|\le|f(\omega)-g(\omega)|+|g(\omega)-x|)
donc
-x|<\epsilon\}\le m\{\omega\in\Omega\,|\,|g(\omega)-x|<\epsilon\})
car
-g(\omega)|\}=0)
(les fonctions sont égales m-pp)
idem de pour l'autre inegalité.
les mesures st egales, d'ou le resultat.
C'est bon ça?
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 24 Déc 2009, 09:15
C'est tout à fait juste, mais à mon avis, une preuve du type :
L'ensemble
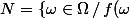\not=g(\omega)\})
est de mesure nulle donc
-x|<\epsilon\}\ =\ m\{\omega\in\Omega\backslash N\,/\,|f(\omega)-x|<\epsilon\}\ =\ m\{\omega\in\Omega\backslash N\,/\,|g(\omega)-x|<\epsilon\}\ =\ m\{\omega\in\Omega\,/\,|g(\omega)-x|<\epsilon\})
Montrerais mieux que la formule aprés le "tel que" n'a pas une grande importance dans la preuve...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
