s'il vous plait, quelqu'un pourrait-il me faire la démonstration de ces identités
Bien cordialement.
Identités
4 messages
- Page 1 sur 1
par capitaine nuggets » 06 Juin 2014, 20:41
Salut !
C'est un forum d'entraide : on ne fera pas le travail à ta place.
Saurais-tu résoudre d'abord dans
l'équation 
?
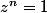
Déduis-en alors une factorisation de
:+++:
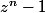
adamNIDO a écrit:bonjour,
s'il vous plait, quelqu'un pourrait-il me faire la démonstration de ces identités
Bien cordialement.
C'est un forum d'entraide : on ne fera pas le travail à ta place.
Saurais-tu résoudre d'abord dans
Déduis-en alors une factorisation de
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
par adamNIDO » 06 Juin 2014, 21:31
soit 
, 
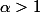
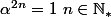
^{2n}=1.e^{i.0} \text{ avec \rho \in \mathbb{R}^{+}_{*},\ \phi \in \mathbb{R}}\\<br />\rho^{2n}.e^{i.2n.\phi}=1.e^{i.0}\\<br />\rho^{2n}=1, \quad e^{i.2n\phi}=e^{i.0}\\<br />\rho=1, \quad 2n.\phi=0[2\pi]\\<br /> \rho=1, \quad \exists k\in \mathbb{Z} \ 2n.\phi=2.k.\pi\\<br /> \rho=1, \quad \phi=\frac{2.k.\pi}{2n} \text{ Alors } \alpha_{k}=e^{i\frac{2.k.\pi}{2n}}\\<br />\text{on pose } k = t + 2nq \text{ ou } t\in \{0,1,\ldots,2n-1\} \text{ et } q \in \mathbb{Z}. \text{ Alors } \alpha_{k}=e^{i\frac{2.t.\pi}{2n}+2.\pi.q}=Z_{t} <br />\\<br />S=\{Z_{k}/k\in \{0,1,\ldots,2n-1\} \})
Pour la deuxième égalité :
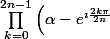 = \left(\prod_{k=0}^0 \dots \quad \cdot \prod_{k=n}^n \dots \right) \left( \prod_{k=1}^{k=n-1} \left(\alpha - e^{\imath \frac{2k\pi}{2n}} \right) \quad \cdot \prod_{k=n+1}^{k=2n-1} \left(\alpha - e^{\imath \frac{2k\pi}{2n}} \right) \right))
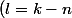j'ai fait un chagement d'indice pour,\quad \prod_{k=n+1}^{k=2n-1} \left(\alpha - e^{\imath \frac{2k\pi}{2n}} \right) =\prod_{k=1}^{k=n-1} \left(\alpha - e^{\imath \frac{(k+n)\pi}{n}} \right))
je suis bloque ici :mur:
Pour la deuxième égalité :
j'ai fait un chagement d'indice pour
par zygomatique » 07 Juin 2014, 18:55
salut
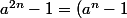(a^n + 1))
il suffit donc de donner les racines n-ièmes de 1 = exp(0i) et de -1 = exp(ipi)
... on remarquera que les seules racines réelles sont 1 et -1 ....
il suffit donc de donner les racines n-ièmes de 1 = exp(0i) et de -1 = exp(ipi)
... on remarquera que les seules racines réelles sont 1 et -1 ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :