Identité remarquable !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Jan 2010, 13:23
par barbu23 » 31 Jan 2010, 13:23
Bonjour à tous : :happy3:
D'habitude, on a :
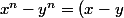 ( \displaystyle \sum_{i=0,...,n-1} x^{i} y^{n-1-i}) $$)
A qui est égale :

 ( \displaystyle \sum_{i=0,...,n-1} \ \ ? ? ? \ \ ) $$)
Merci d'avance ! :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 31 Jan 2010, 13:29
par Nightmare » 31 Jan 2010, 13:29
Salut,
Déjà distinguer n pair ou impair. Une fois que c'est fait, poser y=-Y pour se ramener à la forme précédente si n est impair ou y=iY si n est pair !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Jan 2010, 13:30
par barbu23 » 31 Jan 2010, 13:30
Nightmare a écrit:Salut,
Déjà distinguer n pair ou impair. Une fois que c'est fait, poser y=-Y pour se ramener à la forme précédente si n est impair ou y=iY si n est pair !
On peut ramener les deux cas pair / impair à un seul cas en introduisant le nombre complexe

! non ? :happy3:
mais, comment le faire ? :hum: :happy3:
Merci d'avance ! :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 31 Jan 2010, 13:31
par Nightmare » 31 Jan 2010, 13:31
A priori non.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Jan 2010, 13:32
par barbu23 » 31 Jan 2010, 13:32
Peux tu me donner la formule complète ? :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 31 Jan 2010, 13:33
par Nightmare » 31 Jan 2010, 13:33
Non :lol3:
Je t'ai tout dit, reste plus qu'à remplacer dans la première formule.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Jan 2010, 13:38
par barbu23 » 31 Jan 2010, 13:38
J'ai un peu la flemme de faire des calculs ! :hum: :briques:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Jan 2010, 13:44
par barbu23 » 31 Jan 2010, 13:44
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Jan 2010, 13:45
par barbu23 » 31 Jan 2010, 13:45
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 31 Jan 2010, 13:51
par Nightmare » 31 Jan 2010, 13:51
Déjà, ton indice on va l'appeler k pour éviter de le confondre avec i.
Ensuite,
^{2n-1-k}=\frac{i^{2n}y^{2n}}{i^{1+k}})
Que vaut i^(2n) ? Comment se simplifie

selon les valeurs de k?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Jan 2010, 13:58
par barbu23 » 31 Jan 2010, 13:58
Nightmare a écrit:Déjà, ton indice on va l'appeler k pour éviter de le confondre avec i.
Ensuite,
^{2n-1-k}=\frac{i^{2n}y^{2n}}{i^{1+k}})
Que vaut i^(2n) ? Comment se simplifie

selon les valeurs de k?
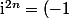^{n} $)
ça je ne sais pas : :hum:

-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 31 Jan 2010, 13:59
par Nightmare » 31 Jan 2010, 13:59
Ben, fais un calcul.
Distingue selon les valeurs de k modulo 4.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Jan 2010, 14:04
par barbu23 » 31 Jan 2010, 14:04
oui, mais là encore il faut distinguer deux cas : pair / impair ! :happy3:
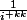
c'est le conjugué de
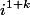
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Jan 2010, 14:36
par barbu23 » 31 Jan 2010, 14:36
svp, un petit coup de main ! :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 31 Jan 2010, 14:38
par Nightmare » 31 Jan 2010, 14:38
Débrouille toi un peu, c'est simplissime comparé à la théorie des corps que tu étudies, tu devrais savoir faire ça quand même :triste:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Jan 2010, 14:43
par barbu23 » 31 Jan 2010, 14:43
Oui, mais toi tu connais la réponse ! pourquoi, je dois la chercher alors ? ça m'ennuie, sincèrement ! Je n'ai pas envie de perdre le temps et abimer ma tête pour rien ! il y'a d'autres trucs plus interessants à faire que ça ! moi, j'étudie une autre théorie plus interessante que ça qui merite d'être appris ! alors, que celà pas du tout ! je ne fais que me casser la tête ! :hum:
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 31 Jan 2010, 14:45
par Skullkid » 31 Jan 2010, 14:45
On dit "et que ça saute", barbu.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Jan 2010, 14:47
par barbu23 » 31 Jan 2010, 14:47
oui, mais ce sera pas grave ! :hum:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 31 Jan 2010, 14:47
par Nightmare » 31 Jan 2010, 14:47
Pourquoi tu dois chercher la réponse? Je sais pas, peut être parce que c'est toi qui nous a dit que tu avais un projet de recherche, et comment veux-tu faire de la recherche si tu ne cherches jamais ? Remets toi en question, ta méthode d'apprentissage est tout sauf bonne.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Jan 2010, 14:50
par barbu23 » 31 Jan 2010, 14:50
Nightmare a écrit:Pourquoi tu dois chercher la réponse? Je sais pas, peut être parce que c'est toi qui nous a dit que tu avais un projet de recherche, et comment veux-tu faire de la recherche si tu ne cherches jamais ? Remets toi en question, ta méthode d'apprentissage est tout sauf bonne.
oui, mais j'ai besoin de la formule maintenant ! happy3: Après, je vais remettre en cause ma methode d'apprentissage ! mais maintenant, je ne pense quà une seule chose ! avoir la formule devant mes yeux ! et ensuite l'appliquer dans mon travail ! :marteau:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités