Bonjour,
je bloque sur ce problème:
Soient un anneau abélien

et
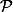
un idéal propre de

. Montrer que
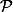
est un idéal premier si et seulement si pour tous idéaux

et

de

on a
(
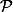
est inclus strictement dans

et dans

)
)
Pour montrer l'implication directe, je n'ai pas eu de problèmes, mais pour l'implication indirecte, j'ai essayé directement de vérifier la définition, par contraposée, par absurde, ça veut pas :briques:
Par exemple si on se fixe
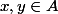
tels que
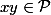
.
On a
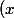.(y) = (xy)\subseteq \mathcal{P})
. D'après (1), on doit avoir ou bien
=\mathcal{P} \mbox{ ou } (x)\not\subset \mathcal{P}])
, ou bien
=\mathcal{P} \mbox{ ou } (y)\not\subset \mathcal{P}])
.
Si
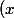=\mathcal{P})
ou
=\mathcal{P})
c'est fini, mais si par exemple
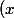\not \subset \mathcal{P})
rien ne nous dit qu'on a
\subset \mathcal{P})
. Là je ne vois pas comment continuer dans le cas où je ne fais pas une fausse piste.
Merci pour vos indications.
