Idéaux premiers

[Pikachue]

Bonjour, j'ai trois petites questions à vous poser sur de l'algèbre.

1) J'ai P un idéal premier de l'anneau des entiers de L, et j'ai b un élément de P.
La norme de b est le produit des , où les sont les éléments du groupe de Galois de l'extension L/K.
Comme l'identité fait partie de ces automorphismes, alors la norme est un élément de P. J'aimerais savoir pourquoi.
On a , (le facteur b est celui donné par l'identité), est-ce que le reste du produit est dans ? (Ce qui expliquerait pourquoi la norme est dans P)

2) Pourquoi cette norme de b est-elle dans ? On sait qu'elle appartient à K par la théorie de Galois, mais pourquoi est-elle dans ?

3)J'ai p un idéal premier de et I un idéal premier à p. On me dit qu'il est aussi premier à P, mais pourquoi?


J'espère avoir donné tout ce qu'il fallait. Sinon, voici le pdf sur lequel je travaille : http://www1.spms.ntu.edu.sg/~frederique/antchap3.pdf
C'est dans la preuve du théorème 3.6 que je bloque, à la page 39.

Merci d'avance.

[Ben314]

Salut,
J'ai pas tout regardé en détail, mais si je comprend bien tout tes corps sont des extensions de Q et le terme "d'entier" désigne systématiquement des entiers sur Z.

Si c'est bien ça, le fait que b soit entier, donc racine d'un polynôme à coeff. dans Z implique que tout ces conjugués le sont aussi (ils sont racine du même polynômes vu que les coeff. sont dans Z donc dans K donc invariant par conjugaison).
Ca répond à tes deux premières questions.

Concernant la 3em question, je comprend pas le sens que ça peut avoir de dire que "P (idéal de OK) soit premier à I (idéal de OL)".
J'aurais tendance à penser qu'il s'agit d'une faute de frappe et qu'il faut lire P.OL dans toute la phrase en question (vérifie que ça colle avec ce qu'il conclue)

[Pikachue]

Hello

Je crois avoir compris pour les deux premières.
b est entier, donc l'est aussi car les coefficients du polynôme annulé en b est à coeff entiers, qui sont fixes par .
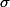
Du coup le produit des (sans l'identité) est dans OL car c'est un anneau (et donc la loi . est interne)
Du coup ça répond à la première question, et pour la deuxième, on ajoute le fait que la norme est dans K, et c'est bon.

Est-ce que c'est bien ça? :we:

Pour la troisième, je me suis mal exprimée, I est un idéal de OL, premier à pOL, et c'est I qui est premier à p (J'ai bien fait une faute de frappe ici, c'est p, pas P).
Si le problème était d'avoir un idéal de OK premier à un idéal de OL, il est toujours là par contre...
Pourtant c'est ce qui est écrit dans le PDF.
Peut-être que p désigne en fait pOL (ça arrive à l'auteur d'écrire p pour pZ par exemple, dans les théorèmes précédents)
Mais ce qu'on dit, c'est que p divise I.A (où A est le produit des ), et on dit que comme I est premier à p, alors p divise A.
Est-ce que, dans ce cas, I premier à pOL implique que p divise A?

[Pikachue]

(Je ne sais pas si j'ai été très claire :/)

[L.A.]

Bonsoir,

en effet, l'auteur a sans doute utilisé p au lieu de pO_L ce qui aurait été plus exact.

[Pikachue]

Bonsoir,

D'accord. C'est vrai que ça paraît plus logique comme ça.

Mais pour le reste? Est-ce que j'ai bon sur la première partie de ma réponse?

(J'ai ma soutenance de mémoire mardi, je suis en train d'exploser intérieurement :marteau: )

[L.A.]

Pour les questions que tu as appelées 1) et 2), oui c'est comme tu l'as dit (le polynôme "annulé en b" ce n'est pas très bien dit, c'est vraiment le polynôme minimal dont on parle ici, qui est à coeffs dans Z)

Pour la question 3) aussi : pour les idéaux on retrouve la plupart des résultats de divisibilité valables dans Z vu que tout idéal se décompose de manière unique en produit d'idéaux premiers à l'ordre près des facteurs.

[Pikachue]

Merci beaucoup!

Je vais faire attention à ce que je dis dans la rédaction au propre de mes questions 1) et 2), c'est vrai que ce n'était pas très bien dit ^^'

Je vais réfléchir à la question 3. Si j'ai besoin d'y revenir, je posterai une nouvelle question.

Merci pour vos réponses, vraiment, ça m'enlève un peu de stresse des épaules :)