D'abord le forum a ete inaccessible pendant quelques heures cette apres midi; Y a-t-il eu un moment d'inaccessibilté momentané ou bien serait-ce mon pc qui bug?
Ensuite j'ai le probleme suivant a soumettre:
Soit k est un corps
Ce qui suit en bleu ne sert pas forcement pour la preuve, mais sait-on jamais!
Si V est un esp. vect. sur k et U un sous esp. vect. de V. Alors:
-A = Endk(V) est un anneau non commutatif (si dimV>1) pour les lois +(plus) et ° (la composition des endomorphismes);
- Ru = {f A/ Im(f) inclus ds U} est un ideal a droite de A;
- Lu = {f A/ U inclus ds ker(f)} est un ideal a gauche de A;
Je veux alors montrer que si A = Mn(k) l'anneau des matrices nxn a coefficients dans k et I est un ideal bilatere non nul de A, alors I = A. J'ai la piste d'utiliser les matrices elementaires Eij pour mq 1A I, mais sans plus!
RadarX.
Ideaux bilateres (et modules??)
7 messages
- Page 1 sur 1
-Avec les matrices élémentaires : calcule pour tout (i,j,k,l) 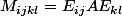 où A est une matrice non nulle de ton idéal I. Remarque que M appartient à I, et que les matrices M engendrent Mn(k).
où A est une matrice non nulle de ton idéal I. Remarque que M appartient à I, et que les matrices M engendrent Mn(k).
-Sinon, remarque que si A appartient à I, toute matrice équivalente à A est dans I aussi. I est non nul, donc contient une matrice de rang r, donc contient (facile à montrer) toute matrice diagonale avec r 1 et n-r 0, donc, en les additionnant astucieusement, une matrice inversible, donc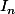 .
.
-Sinon, remarque que si A appartient à I, toute matrice équivalente à A est dans I aussi. I est non nul, donc contient une matrice de rang r, donc contient (facile à montrer) toute matrice diagonale avec r 1 et n-r 0, donc, en les additionnant astucieusement, une matrice inversible, donc
Zeitblom a écrit:-Avec les matrices élémentaires : calcule pour tout (i,j,k,l)où A est une matrice non nulle de ton idéal I. Remarque que M appartient à I, et que les matrices M engendrent Mn(k).
-Sinon, remarque que si A appartient à I, toute matrice équivalente à A est dans I aussi. I est non nul, donc contient une matrice de rang r, donc contient (facile à montrer) toute matrice diagonale avec r 1 et n-r 0, donc, en les additionnant astucieusement, une matrice inversible, donc.
- Multipier par les Eij et a gauche et a droite :stupid_in ! J'avais multiplié a gauche mais fallait penser a le faire aussi a droite, vu que I est bilatere. Cela me va donc tres bien!
- Pour la methode qui fait appel a la theorie des rangs, elle me plait moins quoique tres elegante: je n'ai pas l'esprit a me rememorer ces histoires en ce moment; on verra ca plus tard!
Sinon les deux me vont bien!
Respects!
help
Le problème ayant été résolu avec brio, on pourrait s'en tenir là, mais j'ai envie de pousser mon idée jusqu'au bout, et de montrer que les idéaux à gauche (resp. à droite) de L(E) sont principaux. Je rappelle que E est de dimension finie (en dimension infinie, j'ai bien peur qu'il y ait des idéaux plus sophistiqués...un exemple serait le bienvenu, si le coeur vous en dit...).
Supposons donc que I est un idéal à gauche de L(E), et appelons F l'intersection des noyaux des éléments de I. Puisque nous sommes en dimension finie, F est déjà l'intersection d'un nombre fini de ces noyaux(*). Je veux montrer qu'en fait F est l'un de ces noyaux. A cette fin, je prouve qu'une intersection F= inter Ker(f2)) , où f1 et f2 sont deux éléments de I, est le noyau d'un élément de I : une récurrence terminera la preuve. Je m'intéresse donc à l'ensemble des endomorphismes f1 +qf2, quand q décrit le corps K (ah oui, au fait, je suppose aussi que K est infini). C'est bien le diable si aucun d'entre eux n'a pour noyau F exactement (**)! or ces endomorphismes sont tous dans I, j'ai donc trouvé un f0 dans I tel que ker(f0)=F. I est alors l'ensemble des f de L(E) dont le noyau contient celui de f0, c'est à dire (***) l'ensemble des g.f0, quand g décrit L(E).
, où f1 et f2 sont deux éléments de I, est le noyau d'un élément de I : une récurrence terminera la preuve. Je m'intéresse donc à l'ensemble des endomorphismes f1 +qf2, quand q décrit le corps K (ah oui, au fait, je suppose aussi que K est infini). C'est bien le diable si aucun d'entre eux n'a pour noyau F exactement (**)! or ces endomorphismes sont tous dans I, j'ai donc trouvé un f0 dans I tel que ker(f0)=F. I est alors l'ensemble des f de L(E) dont le noyau contient celui de f0, c'est à dire (***) l'ensemble des g.f0, quand g décrit L(E).
Un passage au dual montre que les idéaux à droite sont bien ceux qu'on pense, et pour répondre à la question des idéaux bilatères, il suffit de voir que l'équivalence "pour tout f de L(E), Kerf contient F ssi Imf est contenue dans G" n'est possible que si F={0} ou E. (****)
Vous aurez remarqué que je me suis habilement abstenu de prouver certains faits (marqués par des astérisques), tantôt par flemme, tantôt par une malhonnêteté qui m'est caractéristique. J'explique :
(*) première malhonnêteté : je n'arrive pas à prouver correctement le lemme suivant : si E est un espace vectoriel de dimension finie, l'intersection d'une famille quelconque de sous-espaces est égale à l'intersection d'un nombre fini d'entre eux. (j'espère que c'est vrai...). Si le corps est R ou C, le fait que la boule unité est compacte n'y est peut-être pas complètement étranger...bref, j'appelle à l'aide.
(**)deuxième malhonnêteté : j'ai envie de considérer la restriction de f1+qf2 à un supplémentaire G de F (sur lequel les restrictions de f1 et f2 ont des noyaux qui ne se rencontrent qu'en {0} ), et de regarder de près le polynôme en q det(f1+qf2), lequel ne peut pas avoir une infinité de racines...si ses coeff ne sont pas tous nuls (ça serait bien contrariant...). En gros, j'aimerais démontrer le lemme suivant :
si f et g sont deux endomorphismes de E dont les noyaux sont en somme directe, il existe un élément q du corps infini K tel que f1+qf2 soit inversible.
(***)ça, c'est de la flemme. C'est bien connu.
(****)ça, c'est encore de la flemme.
Si vous avez des idées pour me sortir de cette situation intolérable, lâchez-vous...
:briques:
à bientôt
Supposons donc que I est un idéal à gauche de L(E), et appelons F l'intersection des noyaux des éléments de I. Puisque nous sommes en dimension finie, F est déjà l'intersection d'un nombre fini de ces noyaux(*). Je veux montrer qu'en fait F est l'un de ces noyaux. A cette fin, je prouve qu'une intersection F=
Un passage au dual montre que les idéaux à droite sont bien ceux qu'on pense, et pour répondre à la question des idéaux bilatères, il suffit de voir que l'équivalence "pour tout f de L(E), Kerf contient F ssi Imf est contenue dans G" n'est possible que si F={0} ou E. (****)
Vous aurez remarqué que je me suis habilement abstenu de prouver certains faits (marqués par des astérisques), tantôt par flemme, tantôt par une malhonnêteté qui m'est caractéristique. J'explique :
(*) première malhonnêteté : je n'arrive pas à prouver correctement le lemme suivant : si E est un espace vectoriel de dimension finie, l'intersection d'une famille quelconque de sous-espaces est égale à l'intersection d'un nombre fini d'entre eux. (j'espère que c'est vrai...). Si le corps est R ou C, le fait que la boule unité est compacte n'y est peut-être pas complètement étranger...bref, j'appelle à l'aide.
(**)deuxième malhonnêteté : j'ai envie de considérer la restriction de f1+qf2 à un supplémentaire G de F (sur lequel les restrictions de f1 et f2 ont des noyaux qui ne se rencontrent qu'en {0} ), et de regarder de près le polynôme en q det(f1+qf2), lequel ne peut pas avoir une infinité de racines...si ses coeff ne sont pas tous nuls (ça serait bien contrariant...). En gros, j'aimerais démontrer le lemme suivant :
si f et g sont deux endomorphismes de E dont les noyaux sont en somme directe, il existe un élément q du corps infini K tel que f1+qf2 soit inversible.
(***)ça, c'est de la flemme. C'est bien connu.
(****)ça, c'est encore de la flemme.
Si vous avez des idées pour me sortir de cette situation intolérable, lâchez-vous...
:briques:
à bientôt
qq réponses
Bon, je vais répondre à certaines de mes questions, puisque personne n'a daigné s'y intéresser. :ptdr:
Tout d'abord, le lemme qui affirme qu'une intersection d'une famille (Fi) de ss-espaces peut être obtenue comme intersection finie :
si m désigne le minimum des dimensions des intersections d'un nombre fini de Fi, il est clair que toutes les intersections de sous-familles finies qui réalisent ce minimum sont égales (si deux d'entre elles ne l'étaient pas, leur intersection serait de dimension
:briques:
Ensuite, le lemme suivant : si f et g sont deux endomorphismes de E dont les noyaux sont en somme directe, on peut trouver q dans K (le corps de base) tel que f-q.g soit inversible.
Soit G un supplémentaire de Kerg. La restriction de g à G est un automorphisme de G, notons h son inverse. Si on note encore f la restriction de f à G, f.h est un endomorphisme de G. Soit q un élément de K qui ne soit pas dans le spectre de f.h.(c'est possible car K est infini) Alors f.h - q.id est inversible, donc en composant avec g : f-q.g est inversible dans L(G). Sur Kerg, f-q.g est égal à f donc son noyau (comme endom. de Kerg) est réduit à zéro puisque Kerf et Kerg ne se rencontrent qu'en {0}. Donc f-q.g est inversible, et répond à la question.
:briques:
Ce qui achève ma démonstration que les idéaux à gauche de L(E) sont monogènes. Mais il y a peut-être plus simple, et j'attends vos idées.
Tout d'abord, le lemme qui affirme qu'une intersection d'une famille (Fi) de ss-espaces peut être obtenue comme intersection finie :
si m désigne le minimum des dimensions des intersections d'un nombre fini de Fi, il est clair que toutes les intersections de sous-familles finies qui réalisent ce minimum sont égales (si deux d'entre elles ne l'étaient pas, leur intersection serait de dimension
:briques:
Ensuite, le lemme suivant : si f et g sont deux endomorphismes de E dont les noyaux sont en somme directe, on peut trouver q dans K (le corps de base) tel que f-q.g soit inversible.
Soit G un supplémentaire de Kerg. La restriction de g à G est un automorphisme de G, notons h son inverse. Si on note encore f la restriction de f à G, f.h est un endomorphisme de G. Soit q un élément de K qui ne soit pas dans le spectre de f.h.(c'est possible car K est infini) Alors f.h - q.id est inversible, donc en composant avec g : f-q.g est inversible dans L(G). Sur Kerg, f-q.g est égal à f donc son noyau (comme endom. de Kerg) est réduit à zéro puisque Kerf et Kerg ne se rencontrent qu'en {0}. Donc f-q.g est inversible, et répond à la question.
:briques:
Ce qui achève ma démonstration que les idéaux à gauche de L(E) sont monogènes. Mais il y a peut-être plus simple, et j'attends vos idées.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
