Archytas a écrit:Pour ce que j'en sais du produit tensoriel, en considérant
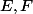
deux A-modules
à gauche on peut former un unique A-module à gauche tel que ...[/tex]
C'est pour ça que je voulais trouver une application bilinéaire ; obtenir un homomorphisme "naturel"
Déjà, à mon avis, faudrait au minimum que tu revois la définition du produit tensoriel (dans le cas non commutatif bien sûr) vu que ça m'étonnerais que tu puisse faire le produit tensoriel de deux A-modules tout les deux
à gauche (ou alors tu tensorise par Z et pas par A). La définition "évidente" dans le cas non commutatif, c'est clairement
\!=\!(xa)\!\otimes\!y)
et ça dit bien ce que ça veut dire...
Archytas a écrit:...tel que pour toute application bilinéaire

avec

un A-module à gauche, on peut trouver une unique application linéaire

telle que
 =f(x,y))
Ensuite, dans le cas non commutatif, "bilinéaire" tout seul, ça veut pas dire grand chose et si tu décrète (par définition) qu'une application bilinéaire f doit vérifier f(x,a.y)=a.f(x,y), tu vois bien que ça va pas marcher vu que tu as fait "commuter" ton a avec le x.
Donc bis et répétat, en non commutatif, le contexte "qui marche bien", c'est celui où E est un B-module à gauche et un A-module à droite et où F est un A-module à gauche et un C-module à droite et où la notion d'application "bilinéaire" est à remplacer par celle de fonction f:ExF->M additives en chaque variables et telles que f(b.x,y)=b.f(x,y) ; f(x.a,y)=f(x,a.y) et f(x,y.c)=f(x,y).c. Évidement tout ça avec M qui est un B-module à gauche et un C-module à droite et où la fameuse unique fonction

va être B-linéaire à gauche et C-linéaire à droite.
Archytas a écrit:Et donc notre application c'est:
)
?
Oui, l'application "bilinéaire" canonique dont on part, c'est effectivement
 \mapsto b\phi(i))
qui est effectivement additive en chaque variable et qui vérifie f(b.x , y) = b.f(x,y) et f(x.a , y) = f(x, a.y).


