Idéaux, anneau quotient

[lapras]

Bonsoir,
je débute dans le domaine des idéaux. J'ai quelques difficultés. En gros j'étudie les anneaux comme celui des entiers de gauss, Z[iV5], etc...
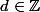
Je me donne , et je pose . Je note une racine de .
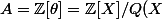Soit (enfin dans la derniere égalité il y a un isomorphisme).
Mon but : trouver les idéaux premiers de contenant où premier dans .
Il semblerait que la réponse soit les où facteur irréductible de dans .
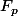
(en projetant tout modulo p, en passant dans les polynomes...)
Mais ca ne me semble pas intuitif, avez vous une démonstration naturelle ?

Lapras

[yos]

Ca dépend de d :

- Il se peut qu'il y ait que (et on dit que p est inerte dans l'extension );

- il se peut qu'il y en ait deux et distincts et du coup (et on dit que p est décomposé);

- il se peut qu'il y en ait un seul P différent de et du coup (et on dit que p est ramifié).

Tout ça dans le cas où est l'anneau des entiers de .

[yos]

Il semblerait que la réponse soit les où facteur irréductible de dans .

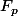
Je crois qu'il faut, comme je l'écrivais plus haut, que soit la clôture intégrale de Z dans . Sinon je doute.

La preuve est juste un peu délicate au niveau des arguments algébriques.

Sinon c'est assez facile à retenir : la décomposition du nombre premier p se reflète dans celle du polynôme minimal de -d modulo p.

[lapras]

Je précise que Z[theta] est l'anneau des entiers de Q(theta).
Je ne sais pas ce qu'est la cloture intégrale...

[yos]

Je précise que Z[theta] est l'anneau des entiers de Q(theta).
Je ne sais pas ce qu'est la cloture intégrale...

C'est pas toujours le cas : c'est le cas quand -d est congru à 2 ou 3 modulo 4 (à vérifier). dans l'autre cas (-d congru à 1 modulo 4), l'anneau des entiers est .

Dire que B est l'anneau des entiers d'un corps L extension de Q revient à dire que B est la cloture intégrale de Z dans L.

[Ben314]

Salut,
Sauf erreur de ma part, si A=Z[X]/(Q) [avec Q irréductible sur Z[X] pour que A soit intègre] et que I est l'idéal engendré par p et M(theta) où p est premier, M un polynôme de Z[X] et theta l'image de X dans la surjection cannonique de Z[X] dans Z[X]/(Q), alors on a isomorphisme entre :
1) A/I
2) Z[X]/(p,Q,M)
3) Fp[X]/(Qp,Mp) où Qp, Mp désignent les images de Q et M par la surjection cannonique de Z[X] dans Fp[X] (i.e. les réductions modulo p)
4) Fp[X]/(pgcd(Qp,Mp))

On a alors :
I est premier <=> A/I est intègre distinct de {0}
<=> pgcd(Qp,Mp) irréductible dans Fp[X] et distinct de 1

P.S. Il me semble que, pour l'exercice, cela ne change rien que Z[theta] soit ou pas l'anneau des entiers de Q[theta]