Soient
Soit
L'idéal des dénominateurs de
Montrer que :
Merci d'avance. :happy3:
Idéal dans un anneau
2 messages
- Page 1 sur 1
Idéal dans un anneau
par barbu23 » 13 Fév 2013, 00:36
Bonsoir,
Soient
un anneau intègre, et  $)
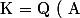son corps de fractions.
Soit
:
L'idéal des dénominateurs de
est par définition :
 = \Big\{ b \in A \ \mid \ bx \in A \Big\} = \Big\{ b \in A \ \mid \ \exists a \in A \ : \ x = \dfrac{a}{b} \ \Big\} \bigcup \{ 0 \} $)
.
Montrer que :
 $)
est un idéal propre 
.
Merci d'avance. :happy3:
Soient
Soit
L'idéal des dénominateurs de
Montrer que :
Merci d'avance. :happy3:
par barbu23 » 13 Fév 2013, 02:27
Bon, il suffit de montrer que :
 = \{ 0 \} $)
ou  = A \ \ \Longleftrightarrow \ \ x \in A $)
.
Ce qui est évident.
Je ne savais que c'était un problème dans la solution est triviale. :hum:
Ce qui est évident.
Je ne savais que c'était un problème dans la solution est triviale. :hum:
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :