Hypothèses Taylor Young

[Elise68]

Bonjour à tous !
J'aimerais avoir votre avis sur un point.
Cela concerne la formule de Taylor Young.
Voilà comme je l'ai énoncée :


Soit I un intervalle de R.
Soit f de classe C^n-1 sur I, tel que f admette une dérivée nième en a.
Alors, pour tout a appartenant à I,
il existe h positif tel que pour tout x appartentant à l'intervalle ouvert a-h;a+h ,
f(x) = (somme habituelle +E(x)(x-a)^n )
où E(x) est une fonction définie sur I tendant vers O en a.

Voici mes questions :
J'ai lu dans un manuel cet théorème où l'hypothèse sur la classe C^n-1 n'était pas mise et d'autre part, il disait que la formule était vraie pour tout x de I.
alors l'hypothèse est-elle de trop?
Est-ce faux comme je l'ai écrit?
J'imagine que cela doit dépendre de la démonstration..
Je le démontre grâce à Taylor Laplace ie Taylor avec reste intégral.

Alors voilà, pouvez vous me dire quelles hypothèses sont indispensables?
Merci beaucoup à vous pour votre aide !! :)

[Nightmare]

Salut :happy3:

En fait l'hypothèse "f admet une dérivée nème en a" suffit effectivement puisqu'elle entraine que f est n-fois dérivables en a et que ses dérivées k-ème avec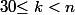 sont continues en a.

Attention par contre pour le reste de Laplace (reste intégral) on a besoin de la continuité de la dérivabilité n-ème en a.

[Elise68]

Ah oui exact !
Donc f admet une dérivée nième en a entraine que f est de classe C^n-1.

Tu veux dire que si je veux démontrer Taylor Young grâce à Taylor avec reste intégral, je dois faire des hypothèses supplémentaires sur f dans Taylor Young?

[Nightmare]

Donc f admet une dérivée nième en a entraine que f est de classe C^n-1

Non attention ! le fait que f admette une dérivée n-ème en a est une propriété locale alors que la classe d'une fonction est une propriété globable.

Oui si tu veux démontrer Taylor-Young par Taylor-Laplace on a besoin de l'hypothèse de la continuité de la dérivée n-ème (en fait, la continuité sur un voisinage du point considéré suffit)

[Elise68]

Donc si je prends :
soit f une fonction admettant une dérivée nième en a tel que sa dérivée nième soit continue sur un voisinage de a.
Alors pour tout a appartenant à ce voisinage on a la formule voulue,

ce théorème est donc juste si j'ai bien compris.
Et il me permet de faire la démonstration en utilisant Laplace.

[Nightmare]

Oui si tu veux :happy3:

Cela dit Taylor-Young peut se démontrer avec le théorème de Rolle sans hypothèses de continuité de la dérivabilité n-ème.

[Nightmare]

Chose importante au passage, il ne faut pas oublier que des fonctions peuvent admettre des DL d'ordre n sans pour autant être n-fois dérivables.