Bonsoir à tous :
Aujourd'hui, je me suis pencher un peu à étudier les coniques et plus précisemment, les hyperboles :
J'ai surtout étudié l'hyperbole
 $)
définie par l'équation :
 : X^2 - Y^2 = 1 $)
.
Une solution parametrique de
 $)
est donnée par :
 \\ <br />Y = \mathrm{sh} ( \theta ) <br />$$)
On a :
 \ , \ (D) : y = \mp \frac{1}{\sqrt{2}} \ , \ e = \sqrt{2} \ , \ A = (\mp 1 , 0 ) \ ) $$)
avec :

: les foyers.
 $)
: les directrices.

: l'excentricité.

: les sommets.
Mon problème est le suivant :
A l'instar des cercles qui sont un cas particulier de coniques ou l'excentricité :
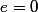
, un point

est défini par :
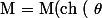,\mathrm{sh} ( \theta )) $)
avec

fixé sur le dessin.
Les fonctions :
 $)
et
 $)
sont définies par des relations géométriques de type :

où

et

sont respectivement les projections de

sur les axes
 $)
et
 $)
.
Par contre, pour l'hyperbole
 $)
, je ne vois pas comment exprimer :
 $)
et
 $)
en fonction de relations géométriques comme c'est le cas de :
 $)
et
 $)
qui ont pour relations géométriques :

Comment donc, exprimer
 $)
et
 $)
en fonction de relations géométriques introduisant,

, et
,P_{y}(M) $)
: qui sont les projections de

sur les axes
 $)
et
 $)
.
Merci d'avance !
