Hyperbole equilatère

[Vuze49]

Bonjour à tous,
je suis confronté au problème suivant :
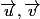
En résumé, je me trouve dans un repère (O ) depuis le début du problème, avec un point P différent de l'origine de coordonnées (a,b) et M un point quelconque de coordonnées (x,y).
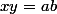
On me demande de déterminer un ensemble sous certaine conditions, et je trouve que M est dans cet ensemble ssi (toujours dans le meme repère).
Puis-je affirmer que l'ensemble cherché est une hyperbole équilatère de centre 0? Pourquoi? Et comment puis-je faire pour déterminer ses asymptotes (je pense qu'il s'agit des axes de coordonnées)?

[Maxmau]

Bj
C'est une hyperbole de centre O lorsque ab différent de zéro
equilatère ss les vecteurs u et v sont orthogonaux

[yos]

En résumé, je me trouve dans un repère (O )

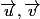
Orthonormé?

avec un point P différent de l'origine de coordonnées (a,b)

Il faudrait que P ne soit pas sur les axes du repère sinon on aurait ab=0 et ton ensemble serait plutôt formé des axes du repère.

Puis-je affirmer que l'ensemble cherché est une hyperbole équilatère de centre 0? Pourquoi? Et comment puis-je faire pour déterminer ses asymptotes (je pense qu'il s'agit des axes de coordonnées)?

Oui, avec les restrictions ci-dessus.
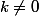
xy=k, avec , est l'équation d'une hyperbole d'asymptotes les axes du repère (se voit au lycée).
Equilatère signifie seuleme,nt que les asymptotes sont perpendiculaires.