Homomorphisme de polinome
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdibj
- Membre Naturel
- Messages: 67
- Enregistré le: 15 Sep 2017, 20:04
-
 par mehdibj » 07 Fév 2021, 19:52
par mehdibj » 07 Fév 2021, 19:52
Bonsoir tout le monde ,
Je bloque sur la démonstration du lemme de Gauss, en faite le seul point qui me bloque est le suivant :
je doit démontrer que
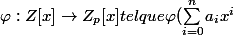=\sum_{i=0}^{n}{\bar{a}_ix^i})
est un Homomorphisme , je sens que la solution est banale mais je bloque depuis un moment donc je pose la question , Merci a tous

-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 07 Fév 2021, 20:16
par GaBuZoMeu » 07 Fév 2021, 20:16
Bonsoir,
Comme tu le dis, c'est banal. Il suffit de se rappeler ce qu'il faut vérifier pour montrer qu'une application est un homomorphisme. Vas-y !
-
mehdibj
- Membre Naturel
- Messages: 67
- Enregistré le: 15 Sep 2017, 20:04
-
 par mehdibj » 07 Fév 2021, 20:25
par mehdibj » 07 Fév 2021, 20:25
GaBuZoMeu a écrit:Bonsoir,
Comme tu le dis, c'est banal. Il suffit de se rappeler ce qu'il faut vérifier pour montrer qu'une application est un homomorphisme. Vas-y !
ce que je fais toujours de faire c'est montré que pour tout a(x),b(x) appartenant a Z[x] :

(a(x)*b(x))=

(a(x))*

(b(x)) mais justement je ne sait pas si je peut dire directement que
*b(x)} =\bar{a(x)}*\bar{b(x)})
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 08 Fév 2021, 13:55
par GaBuZoMeu » 08 Fév 2021, 13:55
Tu peux le dire, mais on te demande de la démontrer.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
