Homomorphisme de groupes

par **barbu23** » 23 Déc 2009, 17:09

Bonjour : :happy3:
J'ai un petit exercice qui me semble un peu difficile à resoudre : :hum:
Soit

un homomorphisme de groupes.
Existe - il un facteur direct

de

d'un groupe

tel que

in duit un isomorphisme de groupes :

tel que le diagramme suivant est commutatif :

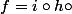
avec

, et

à determiner ?
Merci infiniment ! :happy3:

par **Ben314** » 23 Déc 2009, 21:38

Que devient ta question si par hasard f est injective et que

?
Ne serait tu pas en train de confondre avec la factorisation "cannonique" de tout morphisme de groupe sous la forme :

par **barbu23** » 23 Déc 2009, 22:20

ça donne

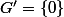
:happy3:

par **Doraki** » 23 Déc 2009, 23:26

Pourtant je connais l'identité : Z -> Z, et Z n'est pas {0}.