Homomorphiseme de groupe et polynome!!
15 messages
- Page 1 sur 1
homomorphiseme de groupe et polynome!!
:we: Bonjour à tous
J'ai une petite question à vous poser. :hein:
Soit S un élément non nul de C(X) mis sous forme irréductible S=B/A, où A et B sont des polynômes non nuls de C[X].
On considère alors l'application f : C[X]->C(X).
R ->R'-SR.
a) Démontrer que f est un homomorphisme de groupes. Ca c'est facile . :id:
b) Déterminer Ker f si :
1) S est un element de C[X].
2) A a un zéro d'ordre au moins deux.
Pour le 1er cas j'ai trouvé que Ker f est constitué par les polynômes qui sont divisibles par leur polynôme dérivé donc kerf est constitué par les polynomes nuls.
pour le deuxiem cas, j'ai trouvé que si a est une racine de A d'ordre au moins deux,alors kerf est constitué par les polynomes R divisible par (X-a)² donc leur derviée R' est divisible par (X-a); mais je ne sais pas comment conclure :hum:
:!: une autre question:
3) on suppose dorénavant que A=produit(i=1..n)(X-ai) oû les ai sont des nombres complexes distincts deux à deux, et on pose pour tout i compris entre 1 et n Ai=A/(X-ai).
calculer Ai(ai) et Ai(aj) avec j different de i. je pense qu'il y a une erreur dans l'enoncé car on ne peut pas calculer Ai(ai) (Ai n'est pas défini en ai)!!
par contre pour Ai(aj) je l'ai trouvé nul.
on admettra que tout polynome de C(n-1)[X] s'écrit de maniere unique come combinaison linéaire des polynomes Ai, i-e sous la forme sigma(i=1..n)kiAi avec ki complexe.
4) soit B element de C*[X] un polynome premier avec A.
Etablir l'équivalence suivante :Kerf est différente du polynome nul <=>
il existe mi avec pour tout i compris entre 1 et n mi est entier NATUREL NON NU tel que B=sigma(i=1..n)miAi.
en fait j'ai démontrer le sens <= de l'équivalence.
car dans la deuxieme question on a trouvé que kerf=O => S appartient àC[X].
donc il suffit de demontrere que C appartient C(X) pour conclure que Kerf differnet de O. ( c'est la contraposée :ptdr: ).
par contre pour l'autre sens :triste:
j'ai suposé que Kerf est différent du { polynome nul }; donc il existe un polynome R non nul appartenat à kerf.donc f(R)=O. d'oû R'=SR
donc R'*A=B*R. donc R divise R'*A or R est premier avec R' car il est non nul donc il divise A. de meme, A divise B*R or A est premier avec B dnc A divise R.
d'oû R=sA oû s est un nombre complexe. et degR=degA=n. => degR'=n-1.
on remplce dans l'egalté precedente on retrouve R'=sB. or R' appartient à
C(n-1)[X] donc R'=sigma(i=1..n)kiAi mais le probleme c'est que ki est complxe
donc je dois seulement montrer que s*ki est entier et le tour est joué.
quelqu'un peut-il m'aider???? :hein: :hein:
:briques: qu'ne pensez vous de ce que j'ai trouvé pour la question (les elements de Kerf).
merci et à plus
:cry:
J'ai une petite question à vous poser. :hein:
Soit S un élément non nul de C(X) mis sous forme irréductible S=B/A, où A et B sont des polynômes non nuls de C[X].
On considère alors l'application f : C[X]->C(X).
R ->R'-SR.
a) Démontrer que f est un homomorphisme de groupes. Ca c'est facile . :id:
b) Déterminer Ker f si :
1) S est un element de C[X].
2) A a un zéro d'ordre au moins deux.
Pour le 1er cas j'ai trouvé que Ker f est constitué par les polynômes qui sont divisibles par leur polynôme dérivé donc kerf est constitué par les polynomes nuls.
pour le deuxiem cas, j'ai trouvé que si a est une racine de A d'ordre au moins deux,alors kerf est constitué par les polynomes R divisible par (X-a)² donc leur derviée R' est divisible par (X-a); mais je ne sais pas comment conclure :hum:
:!: une autre question:
3) on suppose dorénavant que A=produit(i=1..n)(X-ai) oû les ai sont des nombres complexes distincts deux à deux, et on pose pour tout i compris entre 1 et n Ai=A/(X-ai).
calculer Ai(ai) et Ai(aj) avec j different de i. je pense qu'il y a une erreur dans l'enoncé car on ne peut pas calculer Ai(ai) (Ai n'est pas défini en ai)!!
par contre pour Ai(aj) je l'ai trouvé nul.
on admettra que tout polynome de C(n-1)[X] s'écrit de maniere unique come combinaison linéaire des polynomes Ai, i-e sous la forme sigma(i=1..n)kiAi avec ki complexe.
4) soit B element de C*[X] un polynome premier avec A.
Etablir l'équivalence suivante :Kerf est différente du polynome nul <=>
il existe mi avec pour tout i compris entre 1 et n mi est entier NATUREL NON NU tel que B=sigma(i=1..n)miAi.
en fait j'ai démontrer le sens <= de l'équivalence.
car dans la deuxieme question on a trouvé que kerf=O => S appartient àC[X].
donc il suffit de demontrere que C appartient C(X) pour conclure que Kerf differnet de O. ( c'est la contraposée :ptdr: ).
par contre pour l'autre sens :triste:
j'ai suposé que Kerf est différent du { polynome nul }; donc il existe un polynome R non nul appartenat à kerf.donc f(R)=O. d'oû R'=SR
donc R'*A=B*R. donc R divise R'*A or R est premier avec R' car il est non nul donc il divise A. de meme, A divise B*R or A est premier avec B dnc A divise R.
d'oû R=sA oû s est un nombre complexe. et degR=degA=n. => degR'=n-1.
on remplce dans l'egalté precedente on retrouve R'=sB. or R' appartient à
C(n-1)[X] donc R'=sigma(i=1..n)kiAi mais le probleme c'est que ki est complxe
donc je dois seulement montrer que s*ki est entier et le tour est joué.
quelqu'un peut-il m'aider???? :hein: :hein:
:briques: qu'ne pensez vous de ce que j'ai trouvé pour la question (les elements de Kerf).
merci et à plus
:cry:
Pour le 1er cas j'ai trouvé que Ker f est constitué par les polynômes qui sont divisibles par leur polynôme dérivé donc kerf est constitué par les polynomes nuls.
1) Il n'y a qu'un polynôme nul.
2) Un polynôme non nul peut très bien être divisible par son polynôme dérivé : par exemple X, ou X², ou (X-3)². Mais je ne vois pas le rapport avec kerf .
Tu as R'-RS=0 ssi R'=SR. Dans le premier cas (S polynôme), on voit que cela ne peut pas se produire pour des raisons de degré excepté pour le polynôme nul. On a bien ker f ={0} mais pas pour les raisons que tu donnes.
Dans le second cas :
et
Pour la question suivante, je ne crois pas à une erreur car il faut voir que Ai est le polynôme tel que A=(X-ai)Ai.
merci bien YOS.
donc tu dis que je peux calculer Ai(ai)!!! mais Ai=A/(X-ai). :hein: c'est impossible de calculer Ai(ai). car Ai n'est pas défini en ai :triste: .???!!!je crois qu'ils ont fait une erreur dans l'énoncé, je crois que c'est plutôt Aj(ai) tel que j est différent de i.
bon , quant à la dernière question , qu'en penses-tu???
merci :marteau:
donc tu dis que je peux calculer Ai(ai)!!! mais Ai=A/(X-ai). :hein: c'est impossible de calculer Ai(ai). car Ai n'est pas défini en ai :triste: .???!!!je crois qu'ils ont fait une erreur dans l'énoncé, je crois que c'est plutôt Aj(ai) tel que j est différent de i.
bon , quant à la dernière question , qu'en penses-tu???
merci :marteau:
Dans Ai, il n'y a PAS de (X-ai) au dénominateur : c'est seulement une impression!! Ou si tu préfères, on prolonge Ai par continuité en ai. De même qu'on écrit x²/x=x, donc on peut prolonger x²/x en 0 .
La dernière question : on écrit ce qui se passe pour R dans ker f :
AR'=BR et A est premier avec B donc A divise R donc R=AQ, et R'=A'Q+AQ'. Donc A(A'Q+AQ')=BAQ donc A'Q+AQ'=BQ.
On regarde en ai :Q(a_i)+A(a_i)Q'(a_i)=B(a_i)Q(a_i).) .
.
Donc=0) ou bien
ou bien =B(a_i).)
Jusqu'ici, c'est utile pour les deux sens de l'équivalence.
Si R est non nul, alors l'un au moins des) est non nul (degré et nombre de racines). etc.
est non nul (degré et nombre de racines). etc.
La réciproque est pas plus dure.
Quand tu écris "R est premier avec R' car il est non nul ", c'est faux dés que R possède une racine multiple.
La dernière question : on écrit ce qui se passe pour R dans ker f :
AR'=BR et A est premier avec B donc A divise R donc R=AQ, et R'=A'Q+AQ'. Donc A(A'Q+AQ')=BAQ donc A'Q+AQ'=BQ.
On regarde en ai :
Donc
Jusqu'ici, c'est utile pour les deux sens de l'équivalence.
Si R est non nul, alors l'un au moins des
La réciproque est pas plus dure.
Quand tu écris "R est premier avec R' car il est non nul ", c'est faux dés que R possède une racine multiple.
Je reviens pour préciser un peu ce qu'il faut faire.
On exprime B en fonction des Ai :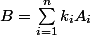 .
.
On suppose que ker f contient un élément non nul R. On doit prouver que les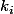 sont entiers >0.
sont entiers >0.
AR'=RB donc A|R donc R=AQ.
D'où A(A'Q+AQ')=AQB, et donc A'Q+AQ'=QB. (égalité (1)).
Supposons que=0) .
.
On factorise Q par^{m_i}) avec
avec 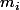 maximum :
maximum :
^{m_i}Q_1) et
et \neq 0) .
.
On remplace dans l'égalité (1) et on simplifie les deux membres par^{m_i}) :
:
Q_1']=BQ_1) .
.
On obtient en appliquant les deux membres en :
:
}=1+m_i) .
.
Donc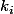 est un entier >0.
est un entier >0.
On exprime B en fonction des Ai :
On suppose que ker f contient un élément non nul R. On doit prouver que les
AR'=RB donc A|R donc R=AQ.
D'où A(A'Q+AQ')=AQB, et donc A'Q+AQ'=QB. (égalité (1)).
Supposons que
On factorise Q par
On remplace dans l'égalité (1) et on simplifie les deux membres par
On obtient en appliquant les deux membres en
Donc
merci bein YOS pour tout le temps que tu m'as consacré :we:
mais je pense qu'avant d'ecrire B sous forme de sigma kiAi il faut d'abord vérifier que B est un polynome de C(n-1)[X], or on ne connait rien sur B.
car seul les polynome de C(n-1)[X] s'écrit de maniere unique comme combinaison linéaire de kiAi??? :marteau:
qu'en penses-tu?? :hein:
mais je pense qu'avant d'ecrire B sous forme de sigma kiAi il faut d'abord vérifier que B est un polynome de C(n-1)[X], or on ne connait rien sur B.
car seul les polynome de C(n-1)[X] s'écrit de maniere unique comme combinaison linéaire de kiAi??? :marteau:
qu'en penses-tu?? :hein:
C'est vrai, mais il faut supposer un truc bien plus fort dés le début de l'exercice : il faut supposer que le degré de B est égal au degré de A plus un, c'est-à-dire que S est de degré -1, sinon l'égalité R'=RS est impossible pour R non nul (pour des raisons de degré).
Autre remarque : dans mon message précédent j'ai traité le cas où Q(ai)=0. L'autre cas que j'ai traité rapidement hier soir (Q(ai) non nul) peut peut-être s'intégrer à ce cas là en prenant mi=0, mais c'est pas certain, il faut tout regarder.
Enfin pour la réciproque, on suppose que B est combinaison des Ai à coef ki entiers >0. On a alors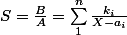 , et on en déduit facilement un élément non nul de ker f en la personne de
, et on en déduit facilement un élément non nul de ker f en la personne de ^{k_i}) (si les ki n'étaient pas entier, ça n'aurait pas de sens).
(si les ki n'étaient pas entier, ça n'aurait pas de sens).
Autre remarque : dans mon message précédent j'ai traité le cas où Q(ai)=0. L'autre cas que j'ai traité rapidement hier soir (Q(ai) non nul) peut peut-être s'intégrer à ce cas là en prenant mi=0, mais c'est pas certain, il faut tout regarder.
Enfin pour la réciproque, on suppose que B est combinaison des Ai à coef ki entiers >0. On a alors
Je viens d'y penser : si tu as vu en cours la décomposition générale de la fraction rationnelle R'/R, tu peux raccourcir certains raisonnements. E effet R est ds ker f ssi R'/R=S. Et tu peux confronter les deux décompositions en éléments simples. Tel que le sujet est présenté, on a l'impression que c'est sans utiliser les décompositions en éléments simples mais je peux me tromper.
:king2: j'avoue que t'es tres doué YOS. t'as raison, car , en fait, l'exercice que j'ai mis à ta disposition est une partie d'un probleme!!
j'ai resolu les 1eres questions dont voila le resultat:
si T et R sont dans C[X] et alors T'/T=R'/R <=> il existe m complexe non nul tel que T=m*R.!!!! oû R est scindé. j'ai démontré aussi que R'/R=sigma(i=1..n) de ci/(X-ai) oû ci est l'ordre de multiplicité des racines de R.
tu sais YOS, j'aimerais bien arriver à ton nivaeu d'analyse d'un probleme de math, car ma seule difficulté en math c'est que je n'arruve pas à saisir la logique d'un probleme!!
donc, comme tu dis,les calculs se simplifiront??? :!:
j'ai resolu les 1eres questions dont voila le resultat:
si T et R sont dans C[X] et alors T'/T=R'/R <=> il existe m complexe non nul tel que T=m*R.!!!! oû R est scindé. j'ai démontré aussi que R'/R=sigma(i=1..n) de ci/(X-ai) oû ci est l'ordre de multiplicité des racines de R.
tu sais YOS, j'aimerais bien arriver à ton nivaeu d'analyse d'un probleme de math, car ma seule difficulté en math c'est que je n'arruve pas à saisir la logique d'un probleme!!
donc, comme tu dis,les calculs se simplifiront??? :!:
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
