Holomorphie

par **kazeriahm** » 28 Mar 2010, 05:52

Bonjour,

un exercie d'analyse complexe sur lequel je butte :

est le disque unite ouvert de

,

est une fonction continue sur

et holomorphe sur

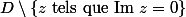
. Montrer que

est holomorphe sur

tout entier.

A ma disposition, je n'ai pas encore de theoreme de prolongement analytique ou de chose comme ca. La seule chose que j'ai et qui se rapproche de ce probleme est que

si f est holomorphe sur U\{z_0} et continue sur U (U ouvert) alors f est holomorphe sur U

ou encore j'ai une caracterisation de l'holomorphie par le fait que l'integrale de f sur tout triangle (sur la frontiere de tout triangle) du domaine doit etre nulle

Ca vous dit quelque chose ?

par **Ben314** » 28 Mar 2010, 11:50

Salut,
Si tu prend un triangle qui ne coupe pas le segment Im(z)=0, c'est O.K.
Si tu prend un triangle qui coupe ce segment, tu coupe le triangle en deux...

par **Doraki** » 28 Mar 2010, 12:16

Et pour un triangle qui a un coté sur la droite Im z = 0, tu le pousses un tout petit peu sur le coté

par **Ben314** » 28 Mar 2010, 12:28

Tient, sans le savoir, notre ami Doraki vient de nous faire part d'une particularité de sa morphologie : les "cotés" de Doraki sont... sa tête et ces pieds... :zen:

par **Doraki** » 28 Mar 2010, 12:42

J'avais pas relu ma phrase c'est vrai qu'elle fait bizarre ^^'

Holomorphie

Holomorphie

Qui est en ligne