Hermitienne

[zork]

bonsoir

dans mon cours d'analyse numérique j'ai:
soit A hermitienne A est définie positive si x*Ax>0

cependant dans mon cours d'algèbre on doit vérifier 2 choses et égalité si X=0 avec - la conjugaison

pourquoi en analyse numérique ce n'est pas pareil au niveau de la définition et de l'écriture, ou sont les conjugués et pourquoi *

merci

[barbu23]

Bonsoir, :happy3:
Si , alors, on a nécessairement , que ce soit définie positive ou non ... donc, c'est facultatif ... Tu la supprimes si tu veux ...
Tu peux garder cette définition :
est définie positive si avec .
Regarde ce qu'il y'a dans ton cours, tu as oublié d'écrire : .
Si, cette condition est verifiée, alors tu as forcement : , et tu as forcément si , que ce soit définie positive ou non ...
Voici des trucs que tu devrais bien connaitre :

Une matrice est définie positive dans est une généralisation de la notion de : Un nombre est strictement positive dans

Si, on travaille dans , alors :

Une matrice est hermitienne si :

[zork]

mais pourquoi il y a une *

et une matrice hermitienne est à coeff complexe donc on devrait toujours mettre la conjugaison pourquoi dans ce que j'ai dis plus haut elle n'y est pas?

[barbu23]

Ta deuxième définition est plus appropriée aux matrices symétriques, par contre, ta première définition est plus appropriée aux matrices hermitiennes ...
S'il s'agit d'une matrice hermitienne , alors :
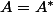
S'il s'agit d'une matrice symétrique , alors :
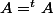
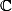
Dans , on parle de matrices hermitiennes.
Dans , on parle de matrices symétriques.
Une matrice hermitienne généralise la notion de matrice symétrique dans .
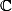
le symbole : est un opérateur ( i.e : Une application linéaire ) qui transforme une matrice complexe, en une matrice adjoint .
On note :
le symbole : est un opérateur ( i.e : Une application linéaire ) qui transforme une matrice réelle, en une matrice transposée .
On note :

[zork]

pourrait tu m'expliquer l'adjoint pour le A*
comment fonctionne-t-il?

[barbu23]

On prend, un exemple :

Alors,

Et donc :

[zork]

je te remercie

[zork]

j'ai encore un truc :

sans la définition d'analyse numérique j'ai x*Ax pourquoi n'y a il pas la conjugaison sur x (dans mon cours d'algèbre c'est comme cela)

et je vois toujours pas pourquoi c'est x*

dans mon cours d'algèbre j'ai comme définition de définie positive

ou est l'étoile là dedans,

[barbu23]

Tu dois peut être poser la question à ton prof ... seul lui peut aider, car c'est lui qui vous a proposé cette définition en classe ...
Voici la définition que je connais moi :
http://fr.wikipedia.org/wiki/Matrice_d%C3%A9finie_positive#Matrice_hermitienne_d.C3.A9finie_positive