DamX a écrit:Hello,
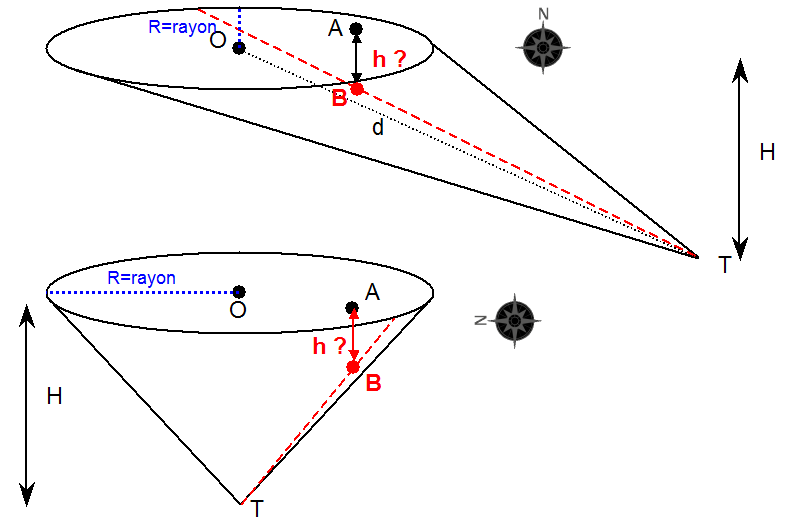
Pour trouver une solution "pas trop" sordide, on se place dans le repére suivant : le sommet du cône est en (0,0,0) le plan xy est celui des sections disques. Et le "biais" du cône (comment le cône se décale par rapport à un cône de révolution) est selon l'axe des "x". Bref dans ce repère, l'equation de ton cône est de la forme :
(x-az)^2 + y^2 = kz^2, où k et a sont des constantes à déterminer.
D'après tes indication, en z=H, le rayon du cercle est R,
Donc on a kH^2 = R^2 d'où k = (R/H)^2
et ta distance D correspond d'après Pythagore à :
(aH)^2 + H^2 = D^2 d'où a^2 = (D/H)^2-1.
On a donc une équation de ton cône parfaitement déterminée.
Partant de là si tu prends A(x,y,H) dans le disque pour z=H (attention ce disque est excentré dans ma parametrisation, tu cherches z tel que B(x,y,z) soit sur le cône, c'est a dire vérifie l'equation.
Ainsi tu as une équation de degré deux en z à résoudre. C'est moche mais ça se fait bien.
L'equation c'est donc résoudre (x-az)^2+y^2=(R/H)^2*z^2 en z qui est ta seule inconnue, je te laisse faire, c'est juste du calcul bourrin de trinôme.
Dans le cas simple où tu as un cône de révolution (a=0), tu trouve directement z^2 = (H/R)^2 * (x^2+y^2).
Damien
---------
Bonjour Damien,
Merci pour ta réponse rapide et claire.
La digestion est un peu moins rapide...
Une intérogation subsiste :
Tu dis que d'après Pythagore à : (aH)² + H² = D²
Or pour mois, d'après Pythagore, j'ai : (Abcisse de O)² + H² = D²
Pourquoi prends-tu aH, plutot que Abcisse de O ?
Avec mes remerciements.
Christophe