capitaine nuggets a écrit:montrer que si E désigne un ensemble,
,\Delta))
est un groupe abélien.
J'ai tenu compte de vos remarque et les ai exploitée.
Stabilité : Soient
)
.
\setminus (A\cap B) \subset A\cup B \in P(E))
, donc

est stable dans
)
;
Element neutre : 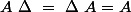
donc

admet dans
)
,

pour élément neutre ;
Symétrique :\setminus (A\cap A)=\empty)
, donc tout élément de
)
est son propre symétrique pour

.
Associativité : 1re méthode : A l'aide de la fonction indicatrice :
En me servant de ton égalité Nightmare :
 \Delta C}=\mathbb{1}_{A\Delta B} + \mathbb{1}_C - 2\mathbb{1}_{A\Delta B} \mathbb{1}_C)
 \mathbb{1}_C)
+4 \mathbb{1}_{A} \mathbb{1}_{B} \mathbb{1}_C))
 }=\mathbb{1}_{A} + \mathbb{1}_{B \Delta C}- 2\mathbb{1}_{A} \mathbb{1}_{B\Delta C })
)
+4 \mathbb{1}_{A} \mathbb{1}_{B} \mathbb{1}_C))
Par suite, on a
 \Delta\ C}=\mathbb{1}_{A \Delta (B \Delta C) })
.
En me servant de ta propriété "Deux ensembles sont égaux si et seulement si leurs fonctions indicatrices associées sont égales", j'en conclut qu'on a
\ \Delta C=A\ \Delta\ (B\ \Delta\ C))
.
Par conséquent, la différence symétrique est bien associative.
2e méthode : mode "brute force"
Je n'y suis pas arrivé, je me noie dans les calculs.
Mon problème vient surement du fait que je ne sais pas trop où je dois aller...
Tes deux propositions m'intéressent Nightmare :
J'ai essayé de démontrer la première, mais bon, ce que j'ai fait me semble un peu foireux par moment :
Proposition 1 : Deux ensembles

et

sont égaux si et seulement si les fonctions indicatrices associées à E et F sont égale, ou encore :
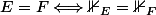
.
)
Supposons que
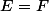
, montrons qu'alors
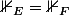
i.e.

.
Par définition de la fonction indicatrice :
-\mathbb{1}_F(x)={ \{ 0-0\ {\rm si}\ x\notin E\ {\rm et}\ x\notin F \\ 0-1\ {\rm si}\ x\notin E\ {\rm et}\ x\in F \\ 1-0\ {\rm si}\ x\in E\ {\rm et}\ x\notin F \\ 1-1\ {\rm si}\ x\in E\ {\rm et}\ x\in F }\<br /><br />=\{ 0\ {\rm si}\ (x\notin E\cup F)\ {\rm ou}\ (x\in E\cap F) \\ 1\ {\rm si}\ (x\notin E\ {\rm et}\ x\in F)\ {\rm ou}\ (x\in E\ {\rm et}\ x\notin F))
Or
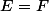
donc les propositions

et

sont équivalentes à

et
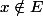
ce qui est faux.
Contrairement à la proposition :
)
qui est équivalente à
)
qui est vraie, donc :
-\mathbb{1}_F(x)=0)
.
)
Supposons que

F, montrons qu'alors
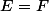
.
= \mathbb{1}_F (x) \Longleftrightarrow \mathbb{1}_E (x)- \mathbb{1}_F(x)=0)
Or
, \mathbb{1}_F(x) \in\mathbb{Z}/2\mathbb{Z}, \mathbb{1}_E (x)- \mathbb{1}_F(x)= 0 \Longleftrightarrow \mathbb{1}_E (x)- \mathbb{1}_F(x)=0\ {\rm ou}\ \mathbb{1}_E (x)- \mathbb{1}_F(x)=1 \Longleftrightarrow (x\notin E\ {\rm et}\ x\notin F)\ {\rm ou}\ (x\in E\ {\rm et}\ x\in F) \Longleftrightarrow (x\in E \Longleftrightarrow x\in F)
Donc
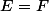
?
Ensuite, j'ai essayé de montré la seconde, mais là je n'y suis pas parvenu :
Proposition 2 : 
.
Merci de m'indiquer une idée de départ.
Enfin, j'aimerais savoir comment faire pour établir des formules comme celles que tu m'as donnée :

,
parce que, pour ma part, j'ai montrer cette égalité en développant les deux membres et en montrant qu'ils sont
égaux, mais comment faire, si l'ont doit partir de

sans avoir d'indice pour obtenir le second membre ?
