Groupes isomorphes

[hoose]

Bonjour,
j'ai une liste de groupe et je dois dire s'ils sont isomorphes cependant il y en a quelques un avec lesquels je ne sais pas comment faire :

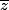
1. l'application z -> est un isomorphisme de C* sur lui même ?

2. l'application x -> est un isomorphisme de R*+ sur lui même ?

3. l'application x -> est un isomorphisme du groupe additif de R sur lui même ?

Merci beaucoup pour votre aide.

4. Même question avec F au lieu de R

[abcd22]

Bonjour,
Un isomorphisme de groupes, c'est une application qui est :
- d'un espace dans lui-même (ça c'est OK) ;
- un morphisme de groupes ;
- bijective (OK).
Reste à te demander si ces applications sont des morphismes de groupes ou pas.

[Imod]

De mon temps isomorphisme signifiait uniquement morphisme bijectif . Quand l'ensemble de départ était aussi l'ensemble d'arrivée on parlait d'automorphisme mais tous cela a peut-être changé :zen:

Imod

[amstramgram]

Je suis assez d'accord avec ça et pourtant je suis encore dans mes études ! :we:

Et puis, c'est plus intéressant d'avoir des ensembles de départ et d'arrivée différents parce que souvent les isomorphismes servent à identifier un groupe (ou un espace vectoriel ou autre) à quelque chose d'autre que l'on peut étudier plus facilement.

Cela dit, tout ça reste du vocabulaire et ici, on peut résoudre le problème que l'on parle d'iso ou d'auto! :we:

[hoose]

mais je ne comprend toujours pas comment par exemple si je prend le premier :
La loi est la multiplication
donc il faut vérifier que le conjugué de (z z') soit égale au conjugué de z fois le conjugué de z' ?

Merci pour votre aide.

[hoose]

mais je ne comprend toujours pas comment par exemple si je prend le premier :
La loi est la multiplication
donc il faut vérifier que le conjugué de (z z') soit égale au conjugué de z fois le conjugué de z' ?

Merci pour votre aide.

[hoose]

mais je ne comprend toujours pas comment par exemple si je prend le premier :
La loi est la multiplication
donc il faut vérifier que le conjugué de (z z') soit égale au conjugué de z fois le conjugué de z' ?

Merci pour votre aide.