Groupe

[wserdx]

e est l'unique élément de G tel que
e * 1/e = 1/e * e = e

Bah, non. La définition du neutre c'est :
pour tout x élément du groupe x * e = e * x = x
L'unicité en découle.

[zork]

je n'ai pas compris ta réponse. Pourquoi me parles tu d'un autre groupes? et pourquoi dis tu qu'il n'y a aucun x et y qui convient?

[Anonyme]

@wserdx
autant pour moi , il faut que je relise mon cours avant d'écrire des conneries sur ce forum de ouf!

[wserdx]

je n'ai pas compris ta réponse. Pourquoi me parles tu d'un autre groupes? et pourquoi dis tu qu'il n'y a aucun x et y qui convient?

Je te propose une approche constructive de ton problème (en quelque sorte je t'apporte la réponse).
Donc j'insiste : étudie le groupe que je te suggère, combien a-t-il d'éléments, quel est son neutre, quelle est sa loi, quel est l'ordre de chacun de ses éléments ?

[wserdx]

Si tu préfères une approche plus directe, pose .
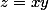
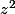
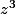
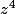
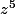
Que valent , , , et ?
(à exprimer en fonction de puissances de x et de y, sans oublier que xy=yx)

[zork]

z²=xy²x
z^3=x
z^4=y
z^5=y²x
z^6=e

mais à quoi sert cela?

[wserdx]

Montre maintenant que tout élément du groupe est de la forme avec et entiers.
Quelles valeurs peuvent prendre et ? Combien d'éléments différents peut-on construire ainsi ?

[zork]

je crois que j'ai compris,

en faites on compose successivement par xy et on regarde les différente valeurs

du coup les éléments de G sont e,x,y,xy²x,y²x

[wserdx]

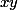
Pas exactement. Je t'ai proposé de calculer les puissances de pour te montrer l'existence d'un élément d'ordre 6.
Réponds plutôt à ma question précédente.
Par exemple peut s'écrire plus simplement. Comment ?

[zork]

xy²x=xyyx=(xy)²=x²y²=y²

[wserdx]

Montre maintenant que tout élément du groupe est de la forme avec et entiers.
Quelles valeurs peuvent prendre et ? Combien d'éléments différents peut-on construire ainsi ?

Peux-tu répondre à cette question ?

[zork]

tu ne peux pas me donner les éléments de G pour que je vois comment on les trouve car ca doit être à peu près la même chose dans tous ces types d'exos

[wserdx]

Je ne vois pas comment on peut te mâcher plus le travail :
Ton groupe est isomorphe au choix (non limitatif) à
-
-
-le groupe des racines complexes 6ème de l'unité,

Maintenant, si tu veux en être convaincu, je ne vois pas mieux que de calculer les éléments de la forme

[zork]

ok je connais la table de (Z6,+)

mais comment as tu su que mon groupe G était isomorphe à (Z6,+)?

[zork]

ca y est je pense avoir compris,

en faites dans la table les éléments doivent être dans G et du coup les éléments de G sont:
e,x,y,y²,xy,xy²

[wserdx]

Oui. Et pourquoi n'y en a-t-il pas d'autres?

[zork]

car l'ordre de G est 6

[wserdx]

car l'ordre de G est 6

Non, ce n'est pas prouvé!

[zork]

dans la suite de l'exo on me demande de montrer que G est cyclique et de donner les sous groupes de G

je sais que G est cyclique s'il est engendré par un seul élément; Mais ici G= du coup il faut que j'exprime par exemple y en fonction de x. Comment faire?

Pour les sous groupes de G, je pense qu'on doit utiliser le théorème de lagrange car tout sous groupe divise l'ordre de G.
J'ai déjà trouvé que {e} est un sous groupe de G. Mais comment trouver le reste,

[zork]

quelle est la raison alors?