Groupe fini d'ordre pair

[Olympus]

Plopouille !

On considère un groupe fini d'ordre pair. On souhaite montrer qu'il existe un élément de ce groupe, différent de son élément neutre , tq .

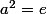
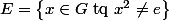
Pour cela, on a donné comme indication de montrer d'abord que le cardinal de est pair.

Si est vide c'est évident, donc on le suppose non vide. Bien évidemment, chaque élément de a son inverse dans . Cela suffirait intuitivement pour en déduire la parité du cardinal de , mais je voulais quelque chose de plus rigoureux, et la meilleure que j'ai pu trouvé c'est celle-ci et je voudrais savoir si y a pas plus simple car j'ai l'impression que c'est un peu long :hum: :

On note le cardinal de et on a bien sûr . On numérote les éléments de comme suit : .

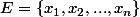
On construit une famille de parties telle que :


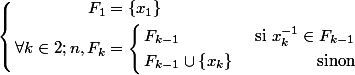
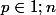
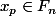
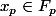
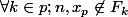
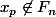
Petit résultat qui sera utilisé dans la suite : Soit . Si alors , car sinon, par construction, on aurait et en particulier , ce qui est absurde.

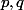
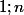
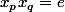
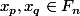
On suppose maintenant qu'il existe deux entiers de tq , et .

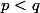
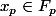
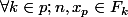
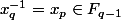
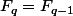
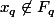
On a , donc et en particulier . Donc et par construction . Ce qui est absurde.

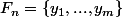
Si on note le cardinal de et si on numérote ses éléments comme suit , alors ce qu'on a montré c'est que . Ainsi, tout élément de a son inverse ailleurs, c'est-à-dire dans .

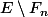
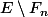
L'ensemble des inverses des éléments de étant inclus dans , et de même cardinal que , on a

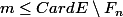
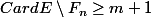
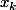
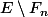
Si , alors il existe un élément de qui n'est l'inverse d'aucun élément de , c'est-à-dire dont l'inverse est aussi dans .

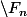
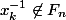
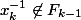
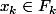
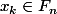
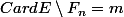
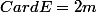
On a , donc en particulier , et par construction , et donc , ce qui est absurde et donc , d'où , et ceci achève notre longue preuve :hein: .

( j'ai le sentiment que je me ferais, évidemment, détruire par une preuve de deux ou trois lignes )

[Maxmau]

Bj
Je reprends ta première idée.
Tout x de E a son inverse ds E et x est différent de son inverse.
E est donc réunion (disjointe) de paires , chaque paire étant constituée d'un élément et de son inverse.
Moi ça me suffit pour conclure que E possède un nombre pair d'éléments.

[Olympus]

Bj
Je reprends ta première idée.
Tout x de E a son inverse ds E et x est différent de son inverse.
E est donc réunion (disjointe) de paires , chaque paire étant constituée d'un élément et de son inverse.
Moi ça me suffit pour conclure que E possède un nombre pair d'éléments.

Salut Maxmau :we:

Merci ! Je sentais bien venir une preuve aussi courte x) L'idée derrière ma preuve était de diviser E en deux parties disjointes, l'une étant constituée des inverses des éléments de l'autre, mais ton découpage en paires est bien plus simple :happy2:

[Maxmau]

Salut Maxmau :we:

Merci ! Je sentais bien venir une preuve aussi courte x) L'idée derrière ma preuve était de diviser E en deux parties disjointes, l'une étant constituée des inverses des éléments de l'autre, mais ton découpage en paires est bien plus simple :happy2:

si vraiment tu veux faire du zèle dans la rigueur en mettant les choses en forme, tu introduis la relation d'équivalence dans E suivante: x équivalent à y ss x est égal à y ou à l'inverse de y
C'est bien une relation d'équivalence
les classes sont des paires de la forme {x, inverse de x}
les classes, donc les paires précédentes, constituent une partition de E

[Doraki]

D'ailleurs dans ta construction, comme tu ne dis pas que parmi les éléments de E, x ne peut pas être son propre inverse, ben tu fais un raisonnement faux.

"supposons xp,xq dans Fn² tel que xp*xq = e et p < q .... contradiction" ok.
"on a montré que pour tout yp,yq dans Fn², yp*yq est différent de e". là non t'as triché.

[Olympus]

Salut Doraki !

tu ne dis pas que parmi les éléments de E, x ne peut pas être son propre inverse

Euh c'est justement la définition de donc je n'ai pas trouvé nécessaire de l'évoquer.

[Doraki]

Si tu ne mentionnes nulle part la définition de E dans ta preuve, le correcteur va penser que tu t'en es pas servi et que pour toi c'est valable pour tout E.
Bon en fait si, la seule chose que tu as dit sur E c'est "chaque élément de E a son inverse dans E".

On pourrait faire un copier-collé de ta preuve en remplaçant E apr E' = {e} union E, on a beaucoup de mal à voir où est-ce que ça coince, parceque l'endroit où tu utilises "chaque élément de E n'est pas son inverse" est caché.

T'aurais juste rajouté un "par définition de E" sur ce passage là, ça passerait oui ; mais là c'est risqué j'trouve.

[Olympus]

@Doraki : En effet, je m'aperçois que j'ai pas très bien rédigé, merci pour la remarque :happy2:
@Maxmau : Jolie l'idée de la relation d'équivalence :happy3:

[Nightmare]

Salut Olympus,

si tu as compris le "principe", tu peux t'attaquer à la généralisation, le fameux théorème de Cauchy :

Si G est un groupe fini d'ordre un multiple d'un nombre premier p, alors il existe un élément de G d'ordre p (ie vérifiant x^p=e).