Groupe des permutations

[azertytreza]

Bonjour et merci d'avance

Dans le cas des groupes symétriques existe t-il un théorème affirmant que

tout groupe des permutations d'un ensemble fini E (groupe symétrique ) possède un sous groupe distingué et équipotent à E?

et dans le cas infini? existe t-il un tel résultat?

[GaBuZoMeu]

Distingué, sûrement pas (vu que le groupe alterné sur cinq éléments ou plus est simple, ça ne va pas marcher dès que le cardinal de E n'est pas tout petit).
Pas distingué, c'est facile (prendre un cycle).

[azertytreza]

Edit : erreur corrigée au post suivant

Merci GabuZoMeu

donc il ne me reste plus que ce résultat :

Le groupe des translations de E (un ensemble non vide et non singleton fini ou non ) d'un espace affine (E,T) avec T un K-espace vectoriel, est un sous groupe du groupe des permutations de E et ce sous groupe est équipotent à E

si on note ce sous groupe de
alors la restriction de l'homomorphisme injectif à est un isomorphisme de T dans

[azertytreza]

je devrais plutôt dire la restriction à T (et pas à )

et terminer en disant que est équipotent à E car T est équipotent à E et l'isomorphisme fait que T est équipotent à

[GaBuZoMeu]

Ma réponse concernait le cas où E est fini.
Si E est infini, que penses-tu du sous-groupe du groupe des permutations de E formé des permutations à support fini (qui sont l'identité en dehors d'une partie finie de E) ?

Je ne comprends pas bien ce que tu écris : E est un ensemble puis un espace affine, je ne vois pas trop où on en est.

[azertytreza]

Merci GaBuZoMeu

En fait j'ai été complètement idiot (quelle perte stupide de temps!)

le seul sous groupe qui est de l'ordre demandé n'est pas normal (justement)

c'est le groupe quotient

Je quitte ce sujet car j'ai beaucoup de travail à faire (sujet résolu)

[GaBuZoMeu]

J'explicite ma suggestion dans le cas d'un ensemble infini .

Soit le groupe des permutations de et soit son sous-groupe des permutations à support fini. Alors :
1°) est un sous-groupe distingué de ,
2°) a même cardinal que (avec l'axiome du choix).

[azertytreza]

GaBuZoMeu , je viens de réaliser que tu traite le cas infini

Il faut que je réfléchisse car rien n'est naturel chez moi (et surtout pas les maths)

Il me faut du temps

[azertytreza]

Merci GaBuZoMeu

je reviens ici pour traiter le cas infini (je suis lent)

pour simplifier l'écriture sera noté

On admettra que E contient

pour simplifier l'écriture je note les permutations qui fixent

sont les permutations qui ne fixent pas 1

sont les permutations qui ne fixent pas 1 et 2

et ainsi de suite…

sont les permutations qui ne fixent pas avec

je reviens plus tard pour voir si j'ai le résultat souhaité

[GaBuZoMeu]

Tu introduis des choses inutiles et qui ne correspondent pas à ce que j'ai décrit.

[azertytreza]

ah je me suis pris la tête pour rien

la composition de deux permutations à support fini est forcément à support fini

et son inverse aussi

la permutation identité est aussi à support finie (son support est vide)

en notant et

pour tout x et y de G

on note relation d'équivalence

si et seulement si 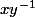est dans H

on note relation d'équivalence compatible avec la loi de groupe

si et seulement si est dans H

on doit vérifier que les deux relations sont compatibles avec G

un moyen simple consiste à montrer que la classe à gauche de tout élément de G est aussi sa classe à droite