Groupe des isométries du cube

[checkmaths]

Bonjour, cette fois-ci, je suis entrain de refaire l'examen de Géométrie de juin 2017


















Et voilà là je suis bloqué, l'algèbre et moi ça fait 2...

Pourriez-vous m'aider svp ?

[capitaine nuggets]

Salut !

OA=OB=OC et h est une isométrie telle que h(O)=O donc Oh(A)=Oh(B)=Oh(C). Or il n'y a pas d'autres points que A, B et C tels que OA=OB=OC donc ...
Le point clé est qu'une isométrie est une transformation qui conserve les longueurs.

Fais un dessin si besoin

[checkmaths]

Je te remercie pour tes conseils, mais est-ce que ça suffit à justifier que est une permutation des sommets , et ?

En fait, je pensais plutôt qu'il fallait montrer que est bijective. Comme ceci :
- injectivité :

- surjectivité : (chose que je n'arrive pas à montrer).

Pourriez-vous m'aider à montrer cette surjectivité svp ?

[capitaine nuggets]

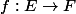
Soit une application telle que les cardinaux de et sont finis non vides et égaux. Alors tu as les équivalences : injective ssi surjective ssi bijective

[checkmaths]

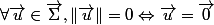
Ah oui c'est vrai merci, mais du coup j'ai montré la bijectivité sans utiliser le fait que ... C'est pas un peu bizarre ? Mon raisonnement a l'air pourtant cohérent puisque et Me serais-je trompé ?

Svp

[capitaine nuggets]

Inutile de poster un message tous les jours pour savoir si quelqu'un peut t'aider. Si quelqu'un veut intervenir, il le fera. Sinon, tu peux toujours chercher davantage de ton côté en attendant.

Relis mon premier post, il faut montrer que justement en utilisant la notion d'isométrie de .

[checkmaths]

Ok d'accord, mais dans ce cas ce que

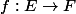
Soit une application telle que les cardinaux de et sont finis non vides et égaux. Alors tu as les équivalences : injective ssi surjective ssi bijective

n'est pas valable pour ? Non ?

[capitaine nuggets]

Si, si tu prouves qu'effectivement l'image de est bien contenue dans . Autrement dit, que les sommets , et , sont bien envoyé dans par .

[checkmaths]

Dans ce cas, j'avais déjà fini psq j'avais montrer l'injectivité plus haut, mais le pb c que je l'ai montré sans utiliser le fait que h(O)=O...