Groupe cyclique et générateur

[mehdi-128]

Bonsoir,


Soit un nombre premier avec . On rappelle que l'ordre d'un entier naturel est le plus petit entier naturel non nul tel que . On le note . On a montré dans une partie précédente que :

On rappelle que si est un nombre premier, l'ensemble muni de la loi induite par la multiplication de est un groupe.

Vérifier que pour ce groupe est cyclique et donner un générateur de ce groupe.
Je pense que j'ai jamais réellement compris la notion de groupe cyclique et de générateur de groupe.

Je vois pas comment faire

[jlb]

As-tu relu l'énoncé? Il y a encore une erreur, je pense!! Sinon, c'est quoi l'ordre d'un élément dans un groupe?

[jlb]

Bon, bah, pas de réponse, bonsoir!

[mehdi-128]

J'ai corrigé la coquille c'est on exclu le je dirais pour avoir une structure de groupe : 0 barre n'admet pas de symétrique pour la loi x.

Considérons le groupe :

Sinon on a : donc

Donc on a si on considère les classes d'équivalence :

est cyclique s'il existe un élément de tel que pour tout il existe un tel que :

On a :

Mais je vois pas comment démontrer dans le cas général que tout élément de peut s'écrire en fonction de

[jlb]

Tu as tapé o(2)=29 dans ton énoncé!! Il y a combien d'éléments dans G? Est-ce possible que 2^k=2^l avec k et l entiers naturels distincts et inférieurs ou égaux à 28? Si tu calcules 2^1, 2^2,....2^28 il y a combien d'éléments? Peuvent-ils être identique modulo 29? Réfléchis à tout cela! Tu devrais comprendre.

[mehdi-128]

possède 28 éléments.

Je crois avoir compris où vous voulez me mener : montrer que les sont distincts 2 à 2 mais j'ai pas trop compris le lien avec le groupe que j'ai introduit.

Il faut montrer que :

Par contraposée ça revient à montrer que :

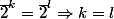
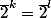
Supposons : alors on a : que l'on peut réécrire :



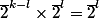
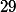
Or est premier avec donc est inversible dans . On multiplie par l'inverse de dans l'égalité et on obtient :



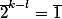
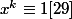
Mais on a montré que l'ordre de divise tout réel qui vérifie donc :

mais et donc forcément

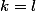
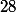
Les sont distincts et au nombre de comme le nombre d'éléments du groupe .

Maintenant comme privé de 0 muni de la multiplication est un groupe

Mon raisonnement est juste ?