Groupe compact et endomorphisme unitaire

[Nightmare]

Salut :happy3:

Puisque mes derniers exercices sur les espace euclid/hermit-ien sont torchés rapidement, j'en propose un autre. La première question n'est pas très difficile (pourtant c'est un exo d'oral d'Ulm, comme quoi !), celle que j'ai rajoutée l'est un peu plus.

On considère un sous-groupe G de .

1) Montrer que si G est fini, il existe un produit scalaire sur qui rendent tous les endomorphismes de G unitaires.

2) Quid du cas où G est un sous-groupe compact?

[ThSQ]

1) a l'air de marcher. C'est pas possible que ce soit aussi simple ?


2) Ca a l'air plus chaud. Ca serait bien d'avoir une sorte d'intégrale sur G :dingue2:

[SimonB]

C'est pas possible que ce soit aussi simple ?

Si, c'est bien ça.

2) Ca a l'air plus chaud. Ca serait bien d'avoir une sorte d'intégrale sur G :dingue2:

Dans le cas d'un groupe compact à un paramètre ça marche tout seul en refaisant avec une intégrale ce qu'on a fait avec cette somme ; dans le cas d'un groupe compact tout seul, je ne sais pas vraiment comment faire.

Joli exercice en tous cas (je l'avais plus ou moins eu en colle l'an dernier).

[skilveg]

Si je me souviens bien, il y a une façon moche de le faire, et une autre en admettant l'existence de la mesure de Haar...

[ThSQ]

Si, c'est bien ça.

Etrange.

Oui, les groupes à un paramètre sont de la forme { e^tA, t € R } (cf exo de prepas.org surlequel je me suis pris le choux l'an dernier !)

[Nightmare]

effectivement on peut y arriver avec les mesures de Haar et l'intégration de Lebesgue. Quelqu'un a-t-il une preuve? :happy3:

[skilveg]

Bah une fois qu'on a une mesure de Haar , c'est trivial que est un bon produit scalaire, non?

[Nightmare]

Oui c'est aussi simple que ça :happy3:

[ThSQ]

Prouver l'existence de la mesure de Haar n'a pas l'air si simple. D'ailleurs trouver une démo ~ compréhensible relève de l'exploit car beaucoup de sites se contentent de "on montre que ...." !

[busard_des_roseaux]

Bj,

je connais rien à votre énoncé (trop difficile) mais je trouve dommage la façon dont il a été "torché".Est-ce un travers de l'université (française) ?
faudrait discuter le bout de gras pour voir en quoi la topologie intervient
(compact ,discret, ça revient ptet pas au même qu'une variété ) lisse, en quoi joue la dimension (il semble qu'il n'y a que S1,S3 et S7 qui soient des sphères avec une structure de groupes de Lie),
comment voir comment le problème est techniquement résolu, comme on obtient cette fameuse mesure de Haar, par recollement,etc ..

parce que là, ça fait un peu bourbakiste...on assène un gros(?) théorème
qui étouffe l'étude. :doh:

[ffpower]

Prouver l'existence de la mesure de Haar n'a pas l'air si simple. D'ailleurs trouver une démo ~ compréhensible relève de l'exploit car beaucoup de sites se contentent de "on montre que ...." !

Je fais essayer de relever l exploit mdr.Bon sérieusement,je vous met la preuve d existence de mesure de Haar sur les groupes compacts que je connais:
Soit G un groupe topologique compact.Petites notations:
Si est une proba sur K et f une fonction continue de K dans R:
-je note
-Si g est dans G, est la fonction f translatée a gauche par g,définie par
-Si g est dans G, est la mesure translatée a gauche par g,définie par ,ou alors par la relation équivalante

est une famille d opérateurs linéaires envoyant probas sur probas,et on veut donc montrer que les ont un point fixe commun.Pour se faire,j'admet l existence d'une proba sur G vérifiant (dans le cas ou G est séparable,qui est le cas qui nous interesse,c est tres facile,on peut prendre pour une somme de diracs.Dans le cas général,je sais pas si c'est facile ou pas..).Une fois qu on dispose d une telle mesure ,on pose alors l opérateur T défini par .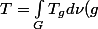C est encore un opérateur envoyant probas sur probas.Et a l instar d a peu pres tous les opérateurs envoyant probas sur probas,T a un point fixe grace a l argument suivant:


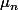
On part d une proba quelconque sur G(par exemple un dirac) et on note . est une suite de probas sur g vérifiant quand n tend vers .On peut extraire de une sous suite convergente vers une proba limite (grace a Banach Alaoglu),et cette proba vérifie


Montrons maintenant que est une mesure de Haar.Soit f une fonction continue fixée de G dans R.Posons .F est a priori une fonction continue de g,et on veut montrer que F est en fait constante.Remarquons que si on translate f a gauche par un certain h,la fonction F correspondante sera elle translatée a droite par h,donc quitte a translater f on peut supposer F maximum en e(=le neutre de G).Par définition de T et de ,on a

Mais F étant max en e,on en déduit que F est constante -presque partout.Comme ,F est donc constante sur un ensemble dense,et par continuité,F est donc constante. est donc bien une mesure de Haar :zen:

[ThSQ]

C'est sympa, merci pour l'effort.

Le truc le plus clair que j'avais trouvé était dans un bouquin de Halmos

[skilveg]

C'est aussi fait dans le livre d'analyse fonctionnelle de Rudin, si je ne m'abuse (et d'ailleurs il faut commencer par justifier l'existence de la mesure de proba dont on part). Je ne sais pas si ça sert quand le groupe est supposé compact mais il me semble que le théorème de point fixe de Kakutani intervient quelque part.

[busard_des_roseaux]

Bj,

on peut poser des questions ?

Pour se faire,j'admet l existence d'une proba sur G vérifiant (dans le cas ou G est séparable,qui est le cas qui nous interesse,c est tres facile,on peut prendre pour une somme de diracs.

Si G est de cardinal infini, on considère une somme de diracs finie ?

on pose alors l opérateur T défini par

on peut avoir des précisions sur cet opérateur ?
est-ce une convolution ?


est une application qui envoie continuement le groupe compact K
sur un groupe (pour la composition) d'automorphismes linéaires de
donc, in fine, on peut additionner ces automorphismes
car, eux, ils agissent sur des fonctions à valeurs réelles ou complexes,
par une addition qui ressemblerait à
c ça ?

autre question:
là, dans ta démo, ffpower, on oublie les hypothèses de Nightmare, à savoir que G est un groupe d'endomorphismes. Içi, on travaille juste avec un groupe abstrait ? il n'y a pas d'espace géométrique sous-jacent
sur lequel opèrent les endomorphismes ? c'est ça ?

dernière question:
est-ce que la topologie intervient, à part la compacité ?
est-ce que l'on peut avoir un groupe topologique qui ait la topologie d'un Cantor ?

merçi d'avance.

[skilveg]

Bonjour,
Quelle insatiable curiosité! :happy2:

est-ce que l'on peut avoir un groupe topologique qui ait la topologie d'un Cantor ?

Il me semble qu'on peut munir d'une structure de groupe topologique le rendant homéomorphe à l'ensemble de Cantor. J'espère ne pas dire trop d'âneries... (Peut-être qu'on peut aussi jeter un oeil du côté des .)

[ffpower]

Bj,

on peut poser des questions ?

Oui :we:

Si G est de cardinal infini, on considère une somme de diracs finie ?

Si G est séparable,et si est une suite dense,on prend par exemple

est une application qui envoie continuement le groupe compact K
sur un groupe (pour la composition) d'automorphismes linéaires de
donc, in fine, on peut additionner ces automorphismes
car, eux, ils agissent sur des fonctions à valeurs réelles ou complexes,
par une addition qui ressemblerait à
c ça ?

C'est en fait les qui sont des automorphismes de ,et ceux la on peut donc bien les additionner comme t a dit. lui agit sur les mesures. translate les fonctions, translate les mesures( est en fait l adjoint de ).Et on peut additionner les mesures,donc on peut aussi additionner les .

"on pose alors l opérateur T défini par "
on peut avoir des précisions sur cet opérateur ?
est-ce une convolution ?

C' est une combinaison convexe des .Si on avait un nombre fini de ,disons ,une combinaison convexe est un truc du type avec .Ici c est pareil sauf que c est une combinaison convexe a priori infinie(et meme indénombrable).Rigoureusement,T est défini par:Si est une mesure sur G,on définit la mesure par

autre question:
là, dans ta démo, ffpower, on oublie les hypothèses de Nightmare, à savoir que G est un groupe d'endomorphismes. Içi, on travaille juste avec un groupe abstrait ? il n'y a pas d'espace géométrique sous-jacent
sur lequel opèrent les endomorphismes ? c'est ça ?

En effet,la je montre juste l existence de mesures de Haar en toute généralité(modulo l existence de ).Je connais aussi une demo directe du résultat initial souhaité,qui s inspire de la demo d existence de mesures de Haar et qui utilise un peu plus le fait que l on travaille sur les matrices,mais je trouve pas cette demo plus simple en fait..

dernière question:
est-ce que la topologie intervient, à part la compacité ?
est-ce que l'on peut avoir un groupe topologique qui ait la topologie d'un Cantor ?
merçi d'avance.

Ta question est "est ce que de tels groupes existent?" ou bien "est-ce que ma demo marche dans de tels groupes?".Dans les 2 cas en tout cas la réponse est oui^^

[busard_des_roseaux]

Ta question est "est ce que de tels groupes existent?" ou bien "est-ce que ma demo marche dans de tels groupes?".Dans les 2 cas en tout cas la réponse est oui^^

ah oui, je me demandais s'il fallait que ces groupes compacts
aient une structure bien lisse comme celles de variétés différentiables
connexes.
je pensais donc à un Cantor comme contre-exemple.
Il n'en est rien.

le procédé est bien intéressant. On doit pouvoir par exemple
approximer la mesure de Lebesgue sur la sphère , en faisant
"tourner",c'est à dire translater, un dirac par le groupe des rotations.
c ça ?

Pour les groupes non compacts, on peut peut être les quotienter, de manière
à obtenir des groupes-quotients compacts, un peu à l'instar des espaces projectifs ?? Mais il faudrait un sous-groupe distingué naturel.


merçi pour tes réponses.