Graphes !

[absolut-diabolik]

bonjour bonjour,

besoin d'un peu d'aide pour montrer que l'on a
Soit G=(S,A) un graphe simple


merci merci beaucoup en fait j'arrive pas à faire une simplification

Je me suis rendue compte que c'était des abhérations d'écrire

ou

Parce que je pensais me servir de

[Doraki]

Dans la somme de gauche, si x est un sommet, combien de fois est-ce que d(x) apparaît ?

[absolut-diabolik]

Dans la somme de gauche, si x est un sommet, combien de fois est-ce que d(x) apparaît ?

x est un des sommets de l'arête a\in A x apparait une seule fois alors ?

[absolut-diabolik]

Dans la somme de gauche, si x est un sommet, combien de fois est-ce que d(x) apparaît ?

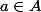
x est un des sommets de l'arête x apparait une seule fois alors ?

[Doraki]

Euh j'ai pas dit que x devait être un sommet d'une arête a particulière.

Dans le graphe S = {0,1,2} avec A = {(0,1) ; (0,2)},
Quand tu écris la somme de gauche, combien de fois est-ce que tu vois d(0) ?

[absolut-diabolik]

2 fois d'abord la somme de d(0)+d(1) pour l'arete {0,1} + d(0)+d(2) pour l'arete {0,2}

mais je vois pas où tu veux en venir... :triste:

[Doraki]

Oui, c'est ça.
Donc dans un graphe général, comment on sait combien de fois est-ce que d(x) apparaît dans la somme ?

Aussi, est-ce que tu sais ce que c'est que d(x) (le degré du sommet x) ?

[absolut-diabolik]

d(x) apparait autant qu'il a de voisins =d(x). J'ai compris ça me fait d²(x)

Mais comment je fais une démonstration rigoureuse de ça ? ..

[Doraki]

Tu dis que tu réordonnes la somme en comptant pour chaque z de S le nombre de fois qu'il apparaît :

où N_z est le cardinal de {(x,y) de A / x=z ou y=z} = d(z).

[absolut-diabolik]

Tu dis que tu réordonnes la somme en comptant pour chaque z de S le nombre de fois qu'il apparaît :

où N_z est le cardinal de {(x,y) de A / x=z ou y=z} = d(z).

Merci je vais faire ça !

[absolut-diabolik]

Toujours dans le même truc on nous demande de prouver que

avec l'inégalité de cauchy swartz mais moi j'ai



G graphe à n sommets et m aretes

[Ben314]

Toujours dans le même truc on nous demande de prouver que

avec l'inégalité de cauchy swartz mais moi j'ai



G graphe à n sommets et m aretes

Je sais pas comment tu montre ton inégalité, mais sur un graphe avec n=4 sommets dont un est relié aux trois autres et c'est tout (donc m=3 arêtes), ton inégalité dit que :
3²+1²+1²+1²<2.3 !!!

Bon, pour prouver le résultat, il faut effectivement utiliser Cauchy-Schwartz.
Je te donne le début :

[absolut-diabolik]

Mais je comprends pas où est passé le n ?

[absolut-diabolik]

Mais je comprends pas où est passé le n ?

bon je vais d'abord tenté avec le début qu'on m'a donné ....

[absolut-diabolik]

Eureka!

Je crois que j'ai fini. :zen:

si j'ai bien compris l'inégalité de CS donne



et d'ap un théorème du cours.

J'espère que j'ai bon ... :hein:

[absolut-diabolik]

Encore une question (la grosse relou :fire: )

G=(S,A) un graphe simple à n sommets et m aretes

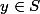
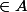
On définit pour tout sommet x de S F(x)={ , {x,y}} l'ensemble des voisins de x dans G


on doit montrer l'inégalité



Par la formule du crible j'ai



avec = (la somme des dégrès donc) 2m ... je crois :doute:

il faut donc que je trouve une majoration entre 2m et n et là :nerf:

:help:

[Ben314]

Un petit "rappel" : ta définition te dit que F(x) et F(y) sont des parties de S, donc la réunion des deux est une partie de S.
Or, combien y-a-t-il d'élément dans S ?

[absolut-diabolik]

n éléments dans S

Mais alors card(F(X)\cup F(y))
J'y comprends plus rien ! :'(

[Ben314]

Un tout petit "rappel" :
Si alors ... :mur:

[absolut-diabolik]

:++:

c'était pas si évident que ça .... Je déconne !!!


Merci ! :king2: