Gödel numbering

[lorenzoL]

Bonjour!Quelqu'un peut m'expliquer comment on peut calculer "the prime factors" d'un numero (1234 par exemple) à l'aide de la numerotation de Gödel?
Merci d'avance!

[mathelot]

Bjr,

un entier naturel peut s'écrire comme
le produit:




où les est la suite des entiers premiers et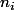
des exposants entiers tous nuls sauf un nombre fini.

L'idée, qui vient de l'algèbre linéaire, est que les
forment une base (dénombrable) et les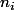 sont en quelque sorte
les "coordonnées" de l'entier n dans cette base.

Gödel a donc une infinité "d'axes de coordonnées" .
Ces axes , cet ensemble dénombrable de dimensions vont lui permettre
de ventiler, d'ordonnancer, de partitonner un ensemble dénombrable,
par exemple, l'ensemble des formules de la logique du 1er ordre,
en l'éclatant sur cet espèce de produit cartésien.


Je n'ai pas lu tout l'article mais il semble qu'il range l'ensemble (dénombrable)
des formules de manière astucieuse, de manière significative.

Il garde donc certains axes de coordonnées pour certains types de formules,
etc..

içi

maintenant, ce qui vient naturellement à l'esprit, c'est de faire la même chose dans ou dans 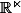, ie,
d'utiliser les tribus, en particulier la tribu borélienne, et de trouver des applications qui "ventileront" les ensembles non dénombrables sur des familles
de sous-ensembles de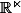 ,familles remarquables du point de vue de la topologie ou de la mesure, comme les intersections d'ouverts denses, et de "remonter" des propriétés de topologies ou de tribus vers des ensembles non dénombrables de formules de la logique du second ordre. Il me semble qu'un logicien associe ainsi des intersections d'ouverts denses à un ensemble d'axiomes et de propositions invariants par le forcing (de Paul Cohen).

[mathelot]

re,

évidemment Gödel s'amuse beaucoup:
1) son application de numérotation
est un petit peu fonctionnelle, en effet:

on pourrait appeler ça un morphisme de concaténation. :zen:

si les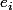 sont des symboles élémentaires (des signes)
et un assemblage de signes.

2) L'application g n'est pas surjective
par ex, le numéro que tu propose 1234 n'est pas un numéro de Gödel.

3) les entiers naturels se retrouvent, et dans l'ensemble de départ de g,
sous forme de constantes du langage, et dans l'ensemble d'arrivée de g,
sous forme de numéro. d'où l'incomplétude d'une théorie formelle
qui comprend comme constantes du langage, les entiers naturels,
obtenue en considérant des formules incluant des constantes entières qui ne sont pas des numéros.

[lorenzoL]

Merci pour votre reponse,en effet l'exercice en question etait de calculer "the prime factors of the number" 45276.

[mathelot]

re,

certains signes très élémentaires , comme les parenthèses,
ont pour numéro les entiers premiers 3,5,7,9,11,13.

Certains assemblages, à la sémantique particulière (constantes, fonctions..)
ont un numéro de Gödel impair.

Les assemblages logiques composites ont un numéro de Godel pair.
On "éclate" ce numéro selon la factorisation en entiers premiers.

on itérère la décomposition et l'analyse syntaxique en considérant la
suite des exposants.
Le problème, je vois pas ce qui se passe quand on tombe sur des exposants égaux à 1.

[mathelot]

coucou,

ici


comme le numéro est pair, c'est le numéro d'une suite d'expressions
comme il y a quatre exposants c'est la suite
de nombres de Godel 2,1,3,1.

Mais c'est impossible car il n'y a pas de nombre de Gödel qui vaut 1.
Donc 45276 n'est pas un numéro.

1)
De deux choses l'une:
- y a un truc que je n'ai pas compris
- ou alors ton exercice fait référence à fonction g différemment définie.

2) questions:
Dans la doc, ils dises que les numéros permettent de distinguer
un symbole d'une expression comportant ce seul symbole
et de même de distinguer une expression d'une suite d'expression(s)
comportant cette seule expression.
du point de vue de la syntaxe, comment distingue t-on dans l'écriture
d'une propriété, un symbole d'une suite comportant ce seul symbole ?

3) qu'est ce qu'une propriété récursive primitive ?
récursive, je vois à peu près, il s'agit d'une propriété qui se "cite"
à l'intérieur de sa syntaxe. Primitive ?