Géométrie plane (mpsi)

[mayele]

J'ai quelques petits soucis avec les questions suivantes du dm:
l'énoncé est : étant donnée une partie X formée de points du plan non tous alignées, on dira que la partie X est orthocentrique si et seulement si tout ortho centre d'un triangle de points de X€X.

Montrer que les parties orthocentriques à 3 éléments sont les sommets d'un triangle rectangle.
j'ai interprété qu'il faut montrer que tt triangle a ses hauteurs qui sont concourantes en l'orthocentre et qui permet de former un triangle rectangle. j'arrive pas à montrer cela analytiquement ?

l'autre question: soit ABC un triangle non rectangle et D son orthocentre.Montrer que {A,B,C,D} est une partie orthocentrique à quatre éléments.

[nuage]

Salut,
si {A,B,C} est une partie orthocentrique alors l'orthocentre du triangle ABC est un des sommets du triangle. Le triangle est donc rectangle car un de ses sommets est sur une (3) hauteur.
Pour la 2° question je te conseille de faire une figure, et d'appliquer le résultat précédent.

[mayele]

Oui mais comment cela se démontre-il ? Seulement ceci suffit ou bien en faisant une figure ça fait preuve de démo ( jpense pas)

[nuage]

Si ABC est orthocentrique alors un des sommets (disons A) est l'orthocentre.
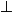
Dans ce cas on a ABAC car A est le pied de la hauteur issue de B (ou de C). Donc le triangle est rectangle en A.

[yos]

Pour la question 2, si H est orthocentre de ABC, alors A est orthocentre de BCH, B est orthocentre de ACH, C est orthocentre de ABH.

[mayele]

Merci de vos réponses donc on voit que chaque pt d'une partie orthocentrique est un orthocentre d'une autre partie orthocentrique et ainsi de suite.

[yos]

Merci de vos réponses donc on voit que chaque pt d'une partie orthocentrique est un orthocentre d'une autre partie orthocentrique et ainsi de suite.

Pas du tout.

[mayele]

Ah non excusez moi de ma betise !!