thoralf8weblen a écrit:Bonjour à tous,
Je viens demander votre aide pour m'aider à résoudre le problème suivant qui pose difficultés.
Ce problème ne me semble pas être d'une difficulté insurmontable mais les raisonnements en géométrie me posent souvent problème. Bref, on y va:
Le plan est rapporté à un repère orthonormé. On donne un triangle par les équations de ses côtés:
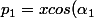+ysin(\alpha_1))
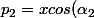+ysin(\alpha_2))
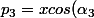+ysin(\alpha_3))
Ecrire les équations des trois hauteurs du triangle et vérifier qu'elles sont concourantes . On ne calculera pas les coordonnées des points.
J'ai essayé d'exprimer les côtés en utilisant le déterminant, en jouant sur le déterminant nul (droites perpendiculaires). Ca n'a rien donné.
Je pense avoir trouvé une combinaison linéaire mais pareil, ça ne mène nulle part. Pourriez-vous m'aider à y voir plus clair. ?
Je vous en remercie d'avance.
Bonjour,
J'ai essayé d'exprimer les côtésLes droites supportant les cotés sont données, il n'y a donc rien à chercher pour "exprimer les cotés".
On peut trouver les coordonnées d'un sommet en résolvant le système de deux équations de cotés.
Par exemple, on a le système :
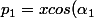+ysin(\alpha_1))
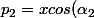+ysin(\alpha_2))
... qui résolu donne les coordonnées du sommet , appelons ce sommet S3
La hauteur issue de S3 est perpendiculaire à la droite d'équation
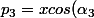+ysin(\alpha_3))
, dont le coefficient directeur est
)
Donc la hauteur a pour coeff directeur
)
Tu as alors le coeff directeur de cette hauteur et les coordonnées du sommet dont elle est issue ... donc tout ce qu'il faut pour en trouver l'équation. (juste prendre garde au cas ou un

est nul ...)
Quand on a l'équation de la hauteur, on peut trouver les 2 autres par simples commutation des indices (des alpha et des p) dans l'équation de la tangente déjà trouvée (toujours prendre garde au cas ou un

est nul ...)
Et ensuite ...

