Géométrie différentielle : champs de vecteurs
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Alain83
- Messages: 2
- Enregistré le: 01 Mai 2012, 14:27
-
 par Alain83 » 01 Mai 2012, 15:03
par Alain83 » 01 Mai 2012, 15:03
Bonjour.
Je n'ai aucun exercice corrigé sur ce cours et j'ai de grosses difficultés avec le cours que l'on m'a fourni.
J'ai donc trouvé cet exercice que j'essaie de résoudre. Merci de votre aide.
a) Sur

on considère les champs de vesteurs
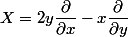
et
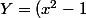\dfrac{\partial}{\partial x}+xy\dfrac{\partial}{\partial y})
De quelle classe sont ces deux champs de vecteurs
Ils sont

?
Où sont le piège, la difficulté ?
J'ai l'impression de ne pas avoir compris cette première question.
Deuxième question
On considère dans

, l'ellipse

d'équation
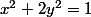
b) Dire rapidement pourquoi

est une

sous-variété compacte de

.
c) Montrer que pour tout

de

et

sont tangents à

(via l'identification canonique de

à un sous-espace vectoriel de

)
b) Soit
=x^2+2y^2-1)
,
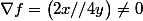
car
\neq(0,0))
Comme

est un fermé borné de

et que
)
est

,

est une

sous variété compacte de

.
-
geegee
- Membre Rationnel
- Messages: 799
- Enregistré le: 11 Mai 2008, 13:17
-
 par geegee » 04 Mai 2012, 17:33
par geegee » 04 Mai 2012, 17:33
Alain83 a écrit:Bonjour.
Je n'ai aucun exercice corrigé sur ce cours et j'ai de grosses difficultés avec le cours que l'on m'a fourni.
J'ai donc trouvé cet exercice que j'essaie de résoudre. Merci de votre aide.
Ils sont

?
Où sont le piège, la difficulté ?
J'ai l'impression de ne pas avoir compris cette première question.
Deuxième question
b) Soit
=x^2+2y^2-1)
,
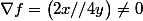
car
\neq(0,0))
Comme

est un fermé borné de

et que
)
est

,

est une

sous variété compacte de

.
Bonjour,
Étant donné un espace vectoriel normé réel ou complexe E (en général de dimension finie, mais pas nécessairement) et U un ouvert de E, une forme différentielle w (de degré 1) de classe Ck sur U est une application de classe de régularité Ck de U dans l'espace dual E* de E. En chaque point u de U,w(u) est donc une forme linéaire, qui peut être appliquée à un vecteur h de E :w(h)(h) est donc un scalaire (un réel ou un complexe).
-
Alain83
- Messages: 2
- Enregistré le: 01 Mai 2012, 14:27
-
 par Alain83 » 05 Mai 2012, 21:28
par Alain83 » 05 Mai 2012, 21:28
Bonjour et merci de m'aider.
Étant donné un espace vectoriel normé réel ou complexe E (en général de dimension finie, mais pas nécessairement) et U un ouvert de E, une forme différentielle w (de degré 1) de classe Ck sur U est une application de classe de régularité Ck de U dans l'espace dual E* de E. En chaque point u de U,w(u) est donc une forme linéaire, qui peut être appliquée à un vecteur h de E :w(h)(h) est donc un scalaire (un réel ou un complexe).
Donc ces deux champs de vecteurs sont de classe

.
Ennoncé a écrit:a) Sur

on considère les champs de vecteurs
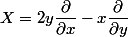
et
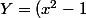\dfrac{\partial}{\partial x}+xy\dfrac{\partial}{\partial y})
De quelle classe sont ces deux champs de vecteurs
Je ne comprends pas

. Je préfèrerai
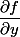
avec
=x)
mais cela signifie la même chose.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
on considère les champs de vesteurs
et
, l'ellipse
d'équation
est une
sous-variété compacte de
.
de
et
sont tangents à
(via l'identification canonique de
à un sous-espace vectoriel de
)
