Géométrie affine euclidienne
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
madameX
- Membre Naturel
- Messages: 17
- Enregistré le: 16 Sep 2007, 08:50
-
 par madameX » 22 Juin 2008, 11:54
par madameX » 22 Juin 2008, 11:54
Bonjour,
on considère les plans P: x+y+z-1=0 et pi: x+2y-z+1=0. Il faut écrire l'équation du plan pi' transformé de pi par rapport à P.
Cela ne doit pas être dur mais je ne sais pas comment commencer.
Merci d'avance
-
mathelot
 par mathelot » 22 Juin 2008, 13:56
par mathelot » 22 Juin 2008, 13:56
bjr,
Il suffit d'écrire la matrice de la symétrie vectorielle

(involutive), de la transposer, et d'appliquer
cette transposée à un vecteur normal de pi pour obtenir un vecteur normal de pi'.
soit
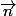
un vecteur normal à pi.
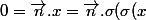))
car

est involutive
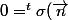.\sigma(x))
)
est un vecteur normal à pi'.
Sauf erreur,
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 22 Juin 2008, 14:22
par yos » 22 Juin 2008, 14:22

conserve le produit scalaire, donc transposer est inutile (endo. symétrique).
On peut aussi décomposer n en
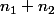
avec
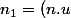u)
et u normal à P. Le symétrique de n est alors

. On achève avec l'image d'un point : par exemple un point de

.
-
mathelot
 par mathelot » 22 Juin 2008, 14:50
par mathelot » 22 Juin 2008, 14:50
MadameX,
je te résume ce qu'a écrit Yos:
Comme la symétrie vectorielle

conserve le produit scalaire
(l'image d'un triangle rectangle est un triangle rectangle),
il suffit de déterminer le symétrique d'un vecteur normal de pi.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
