Geo

[geo]

Salut tout le monde,
mon exercice est le suivant :
J'ai une matrice M de (nm) lignes et m colonnes qui sont linéairement indépendants. On peut la voir comme une matrice formé de n bloc de matrices d'ordre m. Il y a une application qui envoie les déterminants m xm mineurs de M, comme les m colonnes sont linéairement indépendants donc les déterminants ne s'annulent pas tous au même temps.
Supposons que Les n blocs de matrices d'ordre m sont les matrices identités, je voulais savoir combien de déterminants non nul on obtient ?
Merci beaucoup d'avance.

[Ben314]

Salut,
Si je comprend bien ton énoncé, parmi les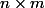 lignes, tu en choisi et tu regarde le déterminant correspondant à ces lignes et aux colonnes.
Donc il y a (coeff. binomial) déterminants possibles et tu voudrait savoir parmi ces déterminants combien sont non nuls (et donc combien sont nuls).

C'est un peu bizarre comme question, mais ça me semble calculable.
Pour que le déterminant soit non nul, il faut choisir une (et une seule) des lignes (1 0 0 ...) ainsi qu'une et une seule des lignes (0 1 0 0 ...) etc...
donc au total,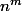 possibilités parmi les choix possibles.

[geo]

Bon au moins j'ai fais le même raisonnement que vous mais j'ai cru qu'il faut multiplié par ( m! ) le nombre de possibilité pour ranger une matrice d'ordre m

[Ben314]

Bon au moins j'ai fais le même raisonnement que vous mais j'ai cru qu'il faut multiplié par ( m! ) le nombre de possibilité pour ranger une matrice d'ordre m

Ca dépend comment tu compte tes sous déterminant :
Est ce que tu considère que le sous-déterminant obtenu avec L1, L2, L3, ... Lm est le même que celui obtenu avec Lm,L(m-1),...,L2,L1 ?
Les valeurs sont les mêmes... au signe prés (donc ils sont tout les deux nuls ou tout les deux non nuls)

Le , et le c'est en considérant que c'est les même.
Si tu considère que c'est pas les même il faut effectivement multiplier par , c'est à dire prendre des "arrangements" et pas des "combinaisons".

[geo]

Ca dépend comment tu compte tes sous déterminant :
Est ce que tu considère que le sous-déterminant obtenu avec L1, L2, L3, ... Lm est le même que celui obtenu avec Lm,L(m-1),...,L2,L1 ?
Les valeurs sont les mêmes... au signe prés (donc ils sont tout les deux nuls ou tout les deux non nuls)

Le , et le c'est en considérant que c'est les même.
Si tu considère que c'est pas les même il faut effectivement multiplier par , c'est à dire prendre des "arrangements" et pas des "combinaisons".

oui Vous avez raison, si non le nombre va étre plus grand méme au nombre total des déterminants. Merci beaucoup ( changer la photo de votre pseudo, si non les gens ne vont pas croire à vos réponses :p je rigole ) Bonne fin de journée.