Generalisation du TAF aux sobolev.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
par MouLou » 09 Oct 2015, 23:16
Bonsoir. Dans un cours j'ai un énoncé dont la démonstration utilise le fait suivant:
si
est un ouvert de
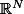
et
)
, alors pour tout
)
-f(y)\mid\leq \mid\mid x-y\mid\mid * \mid\mid grad(f)\mid \mid _{\infty})
.
Est-ce bien vrai et Comment justifie t- on ça?
Dans un bouquin (Brézis) je trouve le théorème de Morrey qui affirme quasiment ceci à une différence:
pour tout p>N, alors pour toute
)
-f(y)\mid\leq \mid\mid x-y\mid\mid^{\alpha} * \mid\mid grad(f)\mid \mid _{L^{p}})
.
Où
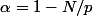
Dans son bouquin, vu la suite, Brezis semble exclure le cas
.
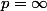
Si vous avez une idée!
-
mathelot
par mathelot » 11 Oct 2015, 12:40
MouLou a écrit:Bonsoir. Dans un cours j'ai un énoncé dont la démonstration utilise le fait suivant:
si
est un ouvert de
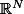
et
, alors pour tout
.
Est-ce bien vrai et Comment justifie t- on ça?
Dans un bouquin (Brézis) je trouve le théorème de Morrey qui affirme quasiment ceci à une différence:
pour tout p>N, alors pour toute
.
Où
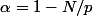
Dans son bouquin, vu la suite, Brezis semble exclure le cas
.
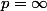
Si vous avez une idée!
dans le Cartan, on paramètre le segment [x;y] via
y)
est un ouvert étoilé
(il existe
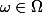
pour tout
)
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
par MouLou » 11 Oct 2015, 21:54
Cartan lui traite le cas d'application C1, dans un ouvert etoilé, ce qui est a peu de chose près comme le cas réel.
Meme dans le cas étoilé, le fait que la fonction soit dérivable au sens des distribution uniquement, cela suffit?
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
par ffpower » 11 Oct 2015, 23:39
Salut. Je pense que l'on peut vérifier effectivement que
y))
est dans
)
, avec
||_\infty\cdot ||x-y||)
Sinon, en methode alternative, si tu sais que l inegalité est vraie dans le cas C1, tu peux utiliser la densité de
)
dans
)
Ou encore, autre methode, si
est borné (on peut se ramener aisément á ce cas), on a
\subset W^{1,p}(\Omega))
, donc on peut utiliser ton inégalité de Morrey puis faire tendre p vers
Sinon, je suis pas convaincu que l'inégalité est valide sur un ouvert quelconque
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
par MouLou » 13 Oct 2015, 22:46
ffpower a écrit:Salut. Je pense que l'on peut vérifier effectivement que
est dans
, avec
Sinon, en methode alternative, si tu sais que l inegalité est vraie dans le cas C1, tu peux utiliser la densité de
dans
Ou encore, autre methode, si
est borné (on peut se ramener aisément á ce cas), on a
, donc on peut utiliser ton inégalité de Morrey puis faire tendre p vers
Sinon, je suis pas convaincu que l'inégalité est valide sur un ouvert quelconque
Oui... le théorème de Morrey n'est donné que sur
...
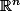
Les deux premières méthodes me conviennent. Merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
