Gauss pour les polynômes

[Victhemath]

Bonsoir, j'ai un exercice qui est le suivant :

Soit p(X) un polynôme p(X)=a0+a1X+...+AnX^n de degré n
avec a0,...,an € Z.
Montrer que si p/q est racine rationnelle de P(X) alors p divise a0 et q divise an.

Help ? Bonne soirée :)

[mrif]

exprime que p/q est racine (à ce propos il manque l'hypothèse p et q premiers entre eux), ensuite tu réduis au même dénominateur.
Pour montrer que que p divise on écrit:
Pour montrer que que q divise on écrit:

[Victhemath]

P et Q sont nécessairement premiers entre eux ? Ce n'est pas dans le poly..

[mrif]

P et Q sont nécessairement premiers entre eux ? Ce n'est pas dans le poly..

Oui.

Pour te convaicre, tu prends le polynome -2 + 3x qui s'annule pour x = 4/6

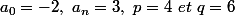
4 ne divise pas -2 et 6 ne divise pas 3.

[Victhemath]

Oui.

Pour te convaicre, tu prends le polynome -2 + 3x qui s'annule pour x = 4/6

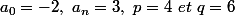
4 ne divise pas -2 et 6 ne divise pas 3.

Super ! Encore merci, la démo est devenue un jeu d'enfant par l'utilisation de gauss
Si j'ai une autre question, je posterai !

[Victhemath]

Le suspense n'aura pas duré longtemps...
Je dois factoriser un polynôme qui est p(X)=18X^4-33X^3+14X^2+3X-2 Comment dois-je faire ? Je dois surement supposer que p/q est racine et trouver p et q à l'aide de Gauss ?

[mrif]

Tu as déjà P(1) = 0 donc tu peux factoriser par x-1, ensuite tu obtiendras:
P(x) = (X-1)Q(x) où Q(x) est un polynome de degré 3 qu'il te faudra déterminer et factoriser en utilisant probablement le résultat précédent.