Bonsoir à tous,
Juste une petite question,
si une fonction f est dans L1(R), sa transformée de Fourier est bien définie.
Mais comment définie-t-on la transformée de Fourier dans L2(R) ?
Fourier dans L2(R)
4 messages
- Page 1 sur 1
Salut,
En fait si alors la transformée de Fourier de
alors la transformée de Fourier de ) est bien définie.
est bien définie.
Le truc est de montrer que est
est 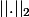 -dense dans
-dense dans  c'est à dire que l'on peut approcher toute fonction
c'est à dire que l'on peut approcher toute fonction 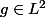 par une suite de fonctions
par une suite de fonctions  dont les transformées de Fourier
dont les transformées de Fourier ) sont bien définies.
sont bien définies.
En travaillant un peu, on peut montrer que pour toute fonction , on a
, on a \in L^2) , on a même
, on a même 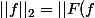||_2) et
et ) est
est 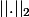 -dense dans
-dense dans  .
.
On peut alors étendre la transformée de Fourier à tout , si
, si  alors on prend une suite
alors on prend une suite  telle que
telle que  ,
, ) est bien définie, appartient à
est bien définie, appartient à  . Puisque
. Puisque 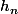 converge c'est une suite de Cauchy dans
converge c'est une suite de Cauchy dans  , puisque
, puisque  est une isométrie de
est une isométrie de  dans
dans 
) est alors aussi une suite de Cauchy dans
est alors aussi une suite de Cauchy dans  qui est complet,
qui est complet, ) converge donc vers une fonction de
converge donc vers une fonction de  que l'on note
que l'on note ) et que l'on définie comme étant la transformée de Fourier de
et que l'on définie comme étant la transformée de Fourier de  .
.
En fait si
Le truc est de montrer que
En travaillant un peu, on peut montrer que pour toute fonction
On peut alors étendre la transformée de Fourier à tout
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
