Formule de Taylor [Résolu]
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
celiaJ
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Oct 2011, 18:25
-
par celiaJ » 20 Oct 2012, 16:02
Bonjour,
Je suis en prépa BCPST1 et j'aurais besoin de votre aide pour comprendre la démonstration de la formule de Taylor que je dois savoir refaire pour ma colle ...
Formule à démontrer :
=\bigsum_{k=0}^{n} \frac{P^{(k)}(\alpha)}{k!}(x-\alpha)^k)
Premier cas :
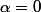
=\bigsum_{k=0}^{n} a_kx^k)
Soit
} = (\bigsum_{k=0}^{n} a_kx^k)^{(j)}= \bigsum_{k=0}^{n} a_k(x^k)^{(j)})
} = \bigsum_{k=0}^{n} a_k(x^k)^{(j)} = \bigsum_{k=j}^{n} \frac{k!}{(k-j)!}a_kx^{k-j})
Ici je n'ai pas compris comment on passe à la dernière égalité.
On fait
. Si
et
D'où il ne reste que le terme pour k=j.
} (0)=a_j\times \frac{j!}{(j-j)!}\times 1=a_j\times j!)
Donc
}(0)}{j!}\times x^k)
On a bien Taylor en 0.
Second cas :
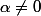
On pose
=P(x+\alpha))
}(x)=P^{(k)}(x+\alpha))
=\bigsum_{k=0}^{n} \frac{Q^{(k)}(0)}{k!}x^k=\bigsum_{k=0}^{n}\frac{P^{(k)}(\alpha)}{k!}x^k)
=P(x -\alpha +\alpha) = Q(x-\alpha))
=\bigsum_{k=0}^{n}\frac{P^{(k)}(\alpha)}{k!}(x- \alpha)^k)
Merci d'avance à ceux qui m'aideront =)
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
par wserdx » 20 Oct 2012, 17:28
-
celiaJ
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Oct 2011, 18:25
-
par celiaJ » 20 Oct 2012, 22:18
D'accord, j'ai compris. Merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
