[Analyse complexe] Formule de Cauchy
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
par Wenneguen » 06 Jan 2015, 20:13
Bonjour,
j'essaye de calculer
} \dfrac{e^z}{z-2} \mathrm{d}z)
où
)
est le cercle complexe centré en 0 et de rayon 1.
Ca semble être une application directe de ce théorème de mon cours :
Théorème : Soit
une fonction holomorphe sur un domaine
,
un compact de
et
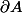
sa frontière. Soit
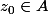
. Alors
=\dfrac{1}{2 \pi i} \displaystyle\oint_{\partial A} \dfrac{f(z)}{z-z_0} \mathrm{d}z)
.
La fonction
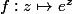
est bien holomorphe sur
. Dans le cas de l'exercice on a
)
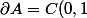, on doit donc avoir nécessairement
)
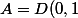, non ? (disque de rayon 1).
Le problème est que pour appliquer le théorème on doit avoir
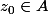
, or
)
.
Comment appliquer ce théorème ?
Merci :we:
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
par Pythales » 06 Jan 2015, 20:46
Wenneguen a écrit:Bonjour,
j'essaye de calculer
où
est le cercle complexe centré en 0 et de rayon 1.
Ca semble être une application directe de ce théorème de mon cours :
La fonction
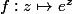
est bien holomorphe sur
. Dans le cas de l'exercice on a
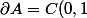, on doit donc avoir nécessairement
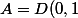, non ? (disque de rayon 1).
Le problème est que pour appliquer le théorème on doit avoir
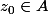
, or
.
Comment appliquer ce théorème ?
Merci :we:
La fonction étant holomorphe sur C et sa frontière, l'intégrale est nulle.
Elle vaut
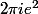
si C a un rayon >2
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
par wobot » 16 Déc 2016, 12:56
