Formes linéaires continues

[legeniedesalpages]

Bonsoir,

je bloque sur cet exercice:

Soient un -espace vectoriel et deux formes linéaires continues sur telles que

[CENTER][/CENTER]

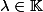
Alors il existe un scalaire tel que .

Merci pour vos indications.

Edit: bon si l'une des deux formes linéaires est nulle c'est ok par contre.

[ffpower]

Soit e tel que phi_1(e) non nul.Tu peux facilement montrer que Ke et ker phi_1 sont supplementaires.Soit k tel que phi_2(e)=k*phi_1(e).Alors phi_2=k*phi_1 sur Ke et sur Ker phi_1,donc sur E

[legeniedesalpages]

merci ffpower,

j'ai donc montré que , par contre je ne vois pas comment on montre que .

Edit: si en fait c'est bon j'ai compris, pour un , on écrit

,

et on a bien ,

[ffpower]

C est ca^^

[legeniedesalpages]

ok merci ffpower, maintenant c'est clair. :)