Forme trigonométrique d'un nombre complexe:
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par Donsalustre69 » 08 Déc 2016, 20:21
par Donsalustre69 » 08 Déc 2016, 20:21
Bonjour à tous,
Je dois mettre sous forme trigo le complexe suivant:
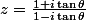
Je multiplie par le conjugué:
^2}{(1-i\tan \theta )(1+i\tan \theta )} \\ \\z=\frac{1+2i\tan \theta-\tan ^2\theta }{1 + \tan ^2\theta } \\ \\z=\frac{1-\tan ^2\theta }{1+\tan ^2\theta }+\frac{2\tan \theta }{1+\tan ^2\theta }i \\ \\z=(1-\tan^2 \theta )\cos^2\theta + 2i\tan \theta \cos ^2\theta \\ \\z=(1 - \frac{\sin ^2\theta }{\cos ^2\theta })\cos ^2\theta + 2i\frac{\sin \theta }{\cos \theta }\cos ^2\theta \\ \\z=\cos ^2\theta -\sin ^2\theta +2i\sin \theta \cos \theta)
Et après je suis bloqué

Quelqu'un peut m'aider ?
Merci
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Déc 2016, 20:40
par Carpate » 08 Déc 2016, 20:40
Formules classiques de passage à l'arc moitié :
=\frac{1-tg^2\theta}{1+tg^2\theta})
=\frac{2tg\theta}{1+tg^2\theta})
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 08 Déc 2016, 21:36
par Pseuda » 08 Déc 2016, 21:36
Bonsoir,
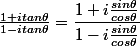
= ... Puis mettre au même dénominateur, et l'argument d'un quotient est égal à la différence des arguments.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 08 Déc 2016, 21:47
par Pisigma » 08 Déc 2016, 21:47
Bonsoir,
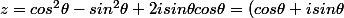^2...)
Autre piste
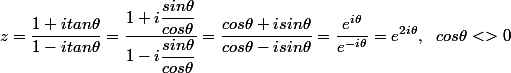
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 08 Déc 2016, 21:48
par Pisigma » 08 Déc 2016, 21:48
grillé par Pseuda
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités

