Forme hermitienne

par **MacManus** » 01 Juin 2008, 22:53

Bonsoir

Je ne me souviens plus quelle(s) méthode(s) appliquer pour faire cet exercice.

Soit

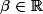
et q la forme quadratique hermitienne définie sur

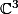
par :

1. Montrer que q est une forme hermitienne dont on donnera la forme sesquilinéaire polaire

2. Pour quelles valeurs de

,

est-elle un produit scalaire ?

Je connais les définitions du cours, mais je n'ai pas assez pratiqué et j'ai fini par oublier le raisonnement.
Quelqu'un peut-il me donner quelques indications pour commencer...
Merci beaucoup

par **Maxmau** » 02 Juin 2008, 11:17

Bj

Ecris q sous la forme :
q(x,y,z) = x ;)1 + y ;)2 +z ;)3 (x = x barre ..etc..)
où ;)1 , ;)2 , ;)3 sont des formes linéaires en x,y,z.
Alors q(x,y,z) = (tV) ;) où tV (transposé de la colonne V) est la ligne (x,y,z) et où ;) est la colonne de composantes : ;)1 , ;)2 , ;)3
Puis ;) = HV où H est hermitienne
Je te laisse terminer

par **MacManus** » 02 Juin 2008, 12:40

Bonjour

Merci Maxmau pour tes explications, j'obtiens d'après ce que tu m'as dit les relations suivantes :

H =

qui est bien hermitienne (la transconjuguée de H est égale à

)

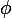
Mais ou sont passés les x', y' et z' ??
Je ne pense pas que mes égalités soient correctes, si ?

Merci beaucoup pour votre aide

par **Maxmau** » 02 Juin 2008, 14:36

Je rectifie (tu aurais pu le faire toi-même)
Ecris q sous la forme :
q(x,y,z) = x ;)1 + y ;)2 +z ;)3 (x = x barre ..etc..)
où ;)1 , ;)2 , ;)3 sont des formes linéaires en x,y,z.
Alors q(x,y,z) = V* ;) où V est la colonne de composantes x,y,z, V* sa transconjuguée (V* est la ligne x,y,z ) et où ;) est la colonne de composantes : ;)1 , ;)2 , ;)3
Puis ;) = HV où H est hermitienne

Lexpression de ;) est exacte mais la ligne précédente est à revoir

J'espère que cette fois-ci je n'ai pas dit de sottises

bon courage

par **MacManus** » 02 Juin 2008, 14:45

Merci beaucoup Maxmau, je suis d'accord. J'avais en fait rectifié sur papier et n'avais pas osé te le montrer... c'est idiot.

Pour la question 2. je sais qu'un produit scalaire sur C est une forme bilinéaire hermitienne définie positive. Je dois calculer les valeur propres de la matrice et montrer qu'elles sont strictement positives, c'est correct ??

par **Maxmau** » 02 Juin 2008, 15:03

MacManus a écrit:Merci beaucoup Maxmau, je suis d'accord. J'avais en fait rectifié sur papier et n'avais pas osé te le montrer... c'est idiot.

Pour la question 2. je sais qu'un produit scalaire sur C est une forme bilinéaire hermitienne définie positive. Je dois calculer les valeur propres de la matrice et montrer qu'elles sont strictement positives, c'est correct ??

ou alors faire une décomposition en "carrés" ...à voir....

par **MacManus** » 02 Juin 2008, 15:19

Je pense que la méthode de réduction en carrés de Gauss est plus appropriée ici, tu as raison. Mais comment faire apparaître ces carrés ? Je veux dire il faut que j'obtienne qqchode de la forme :

q(x,y,z) = . | |² + . | |² + .| |²
il faut avoir le coup d'oeil pour factoriser ... je ne vois pas top comment m'y prendre... as-tu un indice ?

merci encore de bien vouloir me guider!

par **Maxmau** » 02 Juin 2008, 16:32

MacManus a écrit:Je pense que la méthode de réduction en carrés de Gauss est plus appropriée ici, tu as raison. Mais comment faire apparaître ces carrés ? Je veux dire il faut que j'obtienne qqchode de la forme :

q(x,y,z) = . | |² + . | |² + .| |²
il faut avoir le coup d'oeil pour factoriser ... je ne vois pas top comment m'y prendre... as-tu un indice ?

merci encore de bien vouloir me guider!

Je note x = x barre

Tu écris q(x,y,z) = ( x +..) (x + .) + q1(y,z)
Où la deuxième parenthèse est la conjuguée de la première et où q1 est une FQ hermitienne en y,z.
Doù q = |;)1|² + q1(y,z)

1 étant une forme en x,y,z.
Tu continues la réduction avec q1

par **MacManus** » 02 Juin 2008, 17:46

Ok Maxmau merci pour ton aide, la méthode me reviens peu à peu en tête.

Si j'ai bien compris, on a:

où

Donc

a pour valeur 1 logiquement.
C'est bien ça ??
Merci merci

par **MacManus** » 02 Juin 2008, 17:47

zut ...j'ai oublié de réduire q1

par **Maxmau** » 02 Juin 2008, 18:17

MacManus a écrit:Ok Maxmau merci pour ton aide, la méthode me reviens peu à peu en tête.

Si j'ai bien compris, on a:

où

Donc a pour valeur 2 logiquement.
C'est bien ça ??
Merci merci

Et le terme en

|z|² dans l'expression de q(x,y,z) ??
A part çà les calculs semblent bons

Après un calcul rapide (donc à vérifier) je trouve la condition

>2

par **MacManus** » 02 Juin 2008, 18:33

Oui enfin j'ai trouvé mon erreur !

d'où :

d'où la condition que tu as donnée sur

Merci infiniment !

par **MacManus** » 02 Juin 2008, 18:35

Une dernière question si tu le veux bien...

pour réduire en carrés, tu aurais pu choisir une autre expression que celle de

par exemple ?? je veux dire il y a une méthode générale ou pas ? je ne suis pas sûr.

par **Maxmau** » 02 Juin 2008, 19:20

MacManus a écrit:Une dernière question si tu le veux bien...

pour réduire en carrés, tu aurais pu choisir une autre expression que celle de par exemple ?? je veux dire il y a une méthode générale ou pas ? je ne suis pas sûr.

La méthode est générale mais naturellement il n'y a pas unicité du résultat
On aurait pu commencer par considérer les termes en y au lieu des termes en x. C'est une adaptation de la méthode gauss qu'on pratique ds le cas réel

par **MacManus** » 02 Juin 2008, 19:31

D'accord je comprends bien. Merci Maxmau

Forme hermitienne

forme hermitienne

Qui est en ligne