Fonctions sommables sur R ?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 19 Oct 2011, 23:12
par Skullkid » 19 Oct 2011, 23:12
busard_des_roseaux a écrit:c'est pas sommable car
| \neq 0)
Salut, ce n'est pas une justification satisfaisante (outre le fait que |sin| n'a pas de limite en l'infini et donc qu'il est moyennement correct de parler de lim |sin|). La fonction continue affine par morceaux, nulle presque partout (au sens intuitif), qui au-dessus de chaque entier naturel n fait un triangle de hauteur n et de base 2/n^3 est intégrable sur R, mais elle n'a pas de limite en l'infini, et elle atteint même des valeurs aussi grandes qu'on veut.
-
lahass694
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Oct 2011, 16:05
-
 par lahass694 » 19 Oct 2011, 23:30
par lahass694 » 19 Oct 2011, 23:30
J'ai proposé Pi/2 car j'imagine que c'est à cet instant que |sin(t)| voit sa valeur maximale...
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 19 Oct 2011, 23:32
par Skullkid » 19 Oct 2011, 23:32
C'est vrai, mais pourquoi est-ce intéressant de regarder ce qu'il se passe autour des maxima ?
As-tu fait un dessin de la courbe de |sin| ? Est-ce que tu vois, intuitivement, sans le démontrer, pourquoi elle n'est pas intégrable ? Sur ce dessin, tu pourras sans doute voir qu'il est relativement simple de calculer son intégrale entre -a_n et a_n, pour certaines valeurs de a_n.
-
lahass694
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Oct 2011, 16:05
-
 par lahass694 » 19 Oct 2011, 23:50
par lahass694 » 19 Oct 2011, 23:50
Oui je vois la forme de la courbe et intuitivement je dirais entre -Pi, Pi ?
Pourquoi c'est interessant de regarder autour des maxima ? Je n'sais pas trop je dirais car il y a une symétrie dans ce cas là...
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 19 Oct 2011, 23:54
par Skullkid » 19 Oct 2011, 23:54
Oui, exploiter les symétries, et d'une manière générale les propriétés "remarquables" de la courbe est une bonne idée. Mais pour cette courbe-là, la propriété qui est surtout intéressante c'est la périodicité. |sin| est pi-périodique, elle fait la même chose entre 0 et pi, entre pi et 2pi, entre -pi et 0... Donc son intégrale entre 0 et pi va être égale à son intégrale entre pi et 2pi... Vois-tu où je veux en venir ?
-
lahass694
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Oct 2011, 16:05
-
 par lahass694 » 20 Oct 2011, 00:01
par lahass694 » 20 Oct 2011, 00:01
Oui je vois ce que tu veux dire. Par contre même si j'ai les bornes de l'intégrale il faut que je rtouve une primitive de |sin(t)| ?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 20 Oct 2011, 00:21
par Skullkid » 20 Oct 2011, 00:21
Oui et non... Tu ne t'intéresses au final qu'à l'intégrale entre 0 et pi. Et sur cet intervalle, |sin(u)| = sin(u), qui est bien plus agréable.
-
lahass694
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Oct 2011, 16:05
-
 par lahass694 » 20 Oct 2011, 00:38
par lahass694 » 20 Oct 2011, 00:38
Je trouve 0 pour cette intégrale, celle de 0 à PI, ça prouve quelque chose ? :we:
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 20 Oct 2011, 00:44
par Skullkid » 20 Oct 2011, 00:44
lahass694 a écrit:Je trouve 0 pour cette intégrale, celle de 0 à PI, ça prouve quelque chose ? :we:
Ça ne prouve rien. Mais heureusement tu as fait une erreur de calcul, et le bon résultat t'aidera à prouver quelque chose !
-
Anonyme
 par Anonyme » 20 Oct 2011, 07:28
par Anonyme » 20 Oct 2011, 07:28
Bonjour lahass694
Voici un récapitulatif des informations sur l'intégrale sur

de la fonction
=|\sin x|)
(fonction continue donc intégrable sur [-a ,a] avec a un réel quelconque )
C'est une fonction positive qui est

périodique
De plus c'est une fonction paire donc tu devrais pouvoir démontrer le calcul suivant :
Pour tout
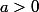
:

Comme elle est

périodique , on a donc
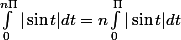
Ces 2 propriétés devraient te permettre de répondre à la question
Remarque:
Cette fonction n'est pas dérivable sur

car elle n'est pas dérivable aux points

avec
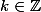
-
lahass694
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Oct 2011, 16:05
-
 par lahass694 » 20 Oct 2011, 07:31
par lahass694 » 20 Oct 2011, 07:31
Oula oui pardon jai trouvé 2. Sa voudrait dire qu'elle tendra vers l'infinie si on augmente les bornes ?
-
Anonyme
 par Anonyme » 20 Oct 2011, 07:51
par Anonyme » 20 Oct 2011, 07:51
lahass694 a écrit:Oula oui pardon jai trouvé 2. Sa voudrait dire qu'elle tendra vers l'infinie si on augmente les bornes ?
OUI
Tu peux même calculer la valeur de l'intégrale

-
lahass694
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Oct 2011, 16:05
-
 par lahass694 » 20 Oct 2011, 08:38
par lahass694 » 20 Oct 2011, 08:38
4n ? vu que de 0 a Pi on a 2, de -Pi a Pi on a 4 ? Donc proportionnel a 4 ?
-
Anonyme
 par Anonyme » 20 Oct 2011, 08:44
par Anonyme » 20 Oct 2011, 08:44
lahass694 a écrit:4n ? vu que de 0 a Pi on a 2, de -Pi a Pi on a 4 ? Donc proportionnel a 4 ?
Oui
.............................
-
lahass694
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Oct 2011, 16:05
-
 par lahass694 » 20 Oct 2011, 09:03
par lahass694 » 20 Oct 2011, 09:03
Merci en tout cas pour cet exercie. Il me reste la fonction exponentielle avec la valeur absolue (e-|t|). Dois je etudier e^t de -inf a 0 et e^-t de 0 a +inf ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 20 Oct 2011, 09:42
par Sylviel » 20 Oct 2011, 09:42
Quelle est ta fonction exactement ? e^(-|t|) ?
Dans ce cas commence par regarder l'intégrale de 0 à +oo de ta fonction.
Puis on regardera sur R.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Anonyme
 par Anonyme » 20 Oct 2011, 09:51
par Anonyme » 20 Oct 2011, 09:51
lahass694 a écrit:Merci en tout cas pour cet exercie. Il me reste la fonction exponentielle avec la valeur absolue (e-|t|). Dois je etudier e^t de -inf a 0 et e^-t de 0 a +inf ?
Bonjour
Etudie la parité de cette fonction et ensuite continue ton étude sur [0 ,+infini[
Question:
Est ce que cette fonction est
=e^{-|x|})
ou
=e^{|x|})
?
car dans ton 1ier message tu as écrit
=e^{|x|})
-
lahass694
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Oct 2011, 16:05
-
 par lahass694 » 20 Oct 2011, 11:00
par lahass694 » 20 Oct 2011, 11:00

C'est bien celle ci.
Sur l'intervalle positif j'ai trouvé que l'intégrale était égale à 1. Je suppose que c'est pareil sur l'intervalle négatif ?*
-
Anonyme
 par Anonyme » 20 Oct 2011, 11:16
par Anonyme » 20 Oct 2011, 11:16
lahass694 a écrit:
C'est bien celle ci.
Sur l'intervalle positif j'ai trouvé que l'intégrale était égale à 1. Je suppose que c'est pareil sur l'intervalle négatif ?*
OUI
Si tu as trouvé que

alors il est très facile d'en déduire que :
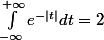
Merci d'expliquer le raisonnement.
-
lahass694
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Oct 2011, 16:05
-
 par lahass694 » 20 Oct 2011, 11:39
par lahass694 » 20 Oct 2011, 11:39
De -Inf à 0 : |(e^|t|)| ~ e^t ; en faisant l'intégrale je trouve e;) - e^-inf = 1
De 0 à +inf : |(e^|t|)| ~ e^-t ; en faisant l'intégrale je trouve -e^-inf + e;) = 1
L'intégrale de -Inf à +Inf = (Intégrale de -Inf à 0) + (Intégrale de 0 à +Inf) = 1 + 1 = 2
Etant donné qu'il s'agit d'une valeur finie je peux conclure que la fonction est sommable :we:
Je remarque que la fonction est paire, il aurait été possible de prouver la parité avant le calcul ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités

